【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,及“凑够一撮人就可以走了,和红绿灯无关”,某校研究性学习小组对全校学生按“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”等三种形式进行调查获得下表数据:
跟从别人闯红灯 | 从不闯红灯 | 带头闯红灯 | |
男生 | 980 | 410 | 60 |
女生 | 340 | 150 | 60 |
用分层抽样的方法,从所有被调查的人中抽取一个容量为![]() 的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ)在所抽取的“带头闯红灯”的人中,任选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有1人是女生的概率.
参考答案:
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)根据分层抽样的抽取比例可求得![]() 值;
值;
(Ⅱ)利用系统抽样的定义求出分段间隔,可得所抽取的![]() 个人的编号,判断抽取的
个人的编号,判断抽取的![]() 人中有
人中有![]() 男
男![]() 女,求得从
女,求得从![]() 人中任选取
人中任选取![]() 人的情况种数,和至少有一名女生的情况种数,利用古典概型的概率公式计算.
人的情况种数,和至少有一名女生的情况种数,利用古典概型的概率公式计算.
试题解析:(Ⅰ)由题意得:![]()
![]() ,
,
解得![]() .
.
(Ⅱ)因为所有参与调查的人数为![]()
![]() ,所以从在“带头闯红灯”的人中用分层抽样抽取的人数为
,所以从在“带头闯红灯”的人中用分层抽样抽取的人数为![]() ,
,
其中男生为![]() 人,女生为
人,女生为![]() 人,设从“带头闯红灯”中抽取的6人中男生用
人,设从“带头闯红灯”中抽取的6人中男生用![]() 表示,女生分别用
表示,女生分别用![]() 表示,则从这6人中任选取2人所有的基本事件为:
表示,则从这6人中任选取2人所有的基本事件为: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 共有15个.这两人均是男生的基本事件为
共有15个.这两人均是男生的基本事件为![]() ,则至少有一个是女生的基本事件共有12个.故从这6人中任选取2人,至少有一个是女生的概率
,则至少有一个是女生的基本事件共有12个.故从这6人中任选取2人,至少有一个是女生的概率![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,
中,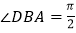 ,
,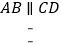 ,
,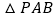 和
和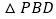 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设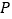 在底面
在底面 的射影为
的射影为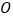 .
.
(1)求证:
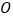 是
是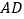 中点;
中点;(2)证明:
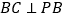 ;
;(3)求点
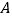 到面
到面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
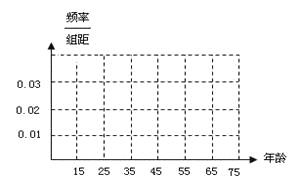
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
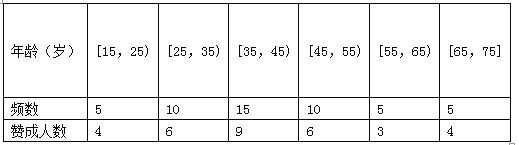
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为
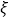 ,求随机变量
,求随机变量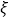 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
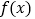 是定义在
是定义在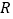 上的偶函数,且对任意的
上的偶函数,且对任意的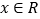 ,都有
,都有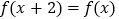 .当
.当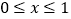 时,
时,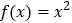 .若直线
.若直线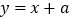 与函数
与函数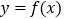 的图象有两个不同的公共点,则实数
的图象有两个不同的公共点,则实数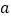 的值是( )
的值是( )A.
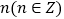 B.
B. 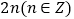
C.
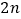 或
或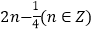 D.
D. 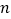 或
或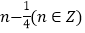
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面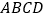 是直角梯形,
是直角梯形,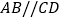 ,
,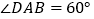 ,
,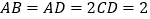 ,侧面
,侧面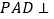 底面
底面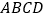 ,且
,且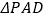 是以
是以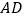 为底的等腰三角形.
为底的等腰三角形.(Ⅰ)证明:
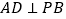
(Ⅱ)若四棱锥
 的体积等于
的体积等于 .问:是否存在过点
.问:是否存在过点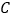 的平面
的平面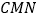 分别交
分别交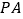 ,
,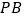 于点
于点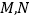 ,使得平面
,使得平面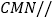 平面
平面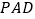 ?若存在,求出
?若存在,求出 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.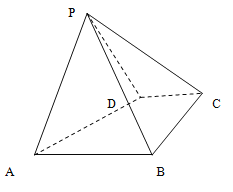
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,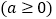 .
.(Ⅰ)若
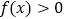 恒成立,求
恒成立,求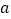 的取值范围;
的取值范围;(Ⅱ)设
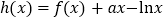 ,
,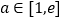 ,(
,(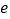 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数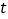 ,使
,使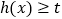 恒成立,若存在,求出
恒成立,若存在,求出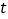 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
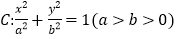 经过点
经过点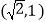 ,且离心率为
,且离心率为 .
.(Ⅰ)求椭圆
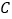 的方程;
的方程;(Ⅱ)设
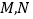 是椭圆上的点,直线
是椭圆上的点,直线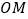 与
与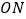 (
(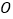 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为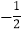 .若动点
.若动点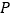 满足
满足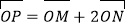 ,试探究是否存在两个定点
,试探究是否存在两个定点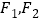 ,使得
,使得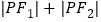 为定值?若存在,求
为定值?若存在,求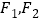 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
相关试题

