【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
参考答案:
【答案】(Ⅰ)见解析(Ⅱ) P=![]() .
.
【解析】试题分析:(Ⅰ)由题意a=20-2-5-4-3-2=4,可依次求得直方图中小矩形的高度从而画出频率直方图.
(Ⅱ)从5人中选取2人的取法有10种,其中2人都小于45岁的有3种,所求概率为P=![]() .
.
试题解析:(Ⅰ)a=20-2-5-4-3-2=4,
直方图中小矩形的高度依次为
![]() =0.02,
=0.02, ![]() =0.04,
=0.04, ![]() =0.05,
=0.05,
![]() =0.04,
=0.04, ![]() =0.03,
=0.03, ![]() =0.02,
=0.02,
频率直方图如图

(Ⅱ)记第五组中的3人为A,B,C,第六组中的2人为a,b,
则从中选取2人的取法有AB,AC,Aa,Ab,BC,Ba,Bb,Ca,Cb,ab共10种,
其中2人都小于45岁的有3种,所以所求概率为P=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
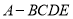 中,底面
中,底面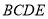 为直角梯形,
为直角梯形, 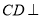 平面
平面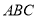 ,侧面
,侧面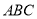 是等腰直角三角形,
是等腰直角三角形, 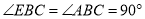 ,
, 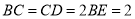 ,点
,点 是棱
是棱 的中点.
的中点.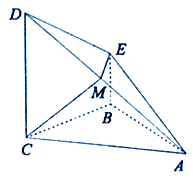
(1)证明:平面
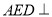 平面
平面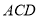 ;
;(2)求锐二面角
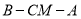 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 被直线
被直线 ,
,  分成面积相等的四个部分,且截
分成面积相等的四个部分,且截 轴所得线段的长为2.
轴所得线段的长为2. (1)求
 的方程;
的方程;(2)若存在过点
 的直线与
的直线与 相交于
相交于 ,
,  两点,且点
两点,且点 恰好是线段
恰好是线段 的中点,求实数
的中点,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
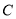 :
:  的焦点为
的焦点为 ,准线为
,准线为 ,三个点
,三个点 ,
,  ,
,  中恰有两个点在
中恰有两个点在 上.
上.(1)求抛物线
 的标准方程;
的标准方程;(2)过
 的直线交
的直线交 于
于 ,
,  两点,点
两点,点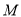 为
为 上任意一点,证明:直线
上任意一点,证明:直线 ,
,  ,
,  的斜率成等差数列.
的斜率成等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知短轴长为2的椭圆
 ,直线
,直线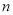 的横、纵截距分别为
的横、纵截距分别为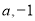 ,且原点到直线
,且原点到直线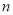 的距离为
的距离为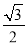 .
.(1)求椭圆
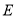 的方程;
的方程;(2)直线
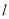 经过椭圆的右焦点
经过椭圆的右焦点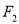 且与椭圆
且与椭圆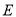 交于
交于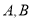 两点,若椭圆
两点,若椭圆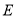 上存在一点
上存在一点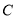 满足
满足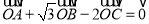 ,求直线
,求直线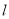 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题
 恒成立;命题
恒成立;命题 方程
方程 表示双曲线.
表示双曲线.(1)若命题
 为真命题,求实数
为真命题,求实数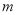 的取值范围;
的取值范围;(2)若命题“
 ”为真命题,“
”为真命题,“ ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,正三棱柱
 的底面边长为2,
的底面边长为2,  是侧棱
是侧棱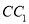 的中点.
的中点.
(1)证明:平面
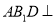 平面
平面 ;
;(2)若平面
 与平面
与平面 所成锐角的大小为
所成锐角的大小为 ,求四棱锥
,求四棱锥 的体积.
的体积.
相关试题

