【题目】如图,四边形![]() 为菱形,四边形
为菱形,四边形![]() 为平行四边形,设
为平行四边形,设![]() 与
与![]() 相交于点
相交于点![]() ,
, ![]() .
.
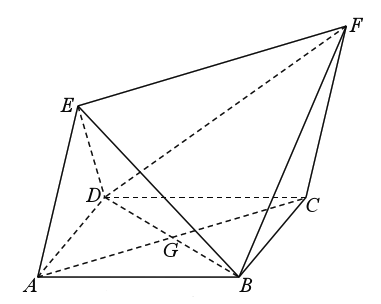
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成角为60°,求二面角
所成角为60°,求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根(1)要证面面垂直,需要找线面垂直,本题中重点分析线段![]() ,利用条件底面是菱形可得
,利用条件底面是菱形可得![]() ,通过全等可知
,通过全等可知![]() ,从而
,从而![]() ,故
,故![]() 是平面
是平面![]() 的垂线,从而得证;(2)涉及二面角的计算,一般需要建系设点,计算平面的法向量,利用二面角与法向量夹角之间的关系处理,需要注意建系时分析清楚哪三条线互相垂直.
的垂线,从而得证;(2)涉及二面角的计算,一般需要建系设点,计算平面的法向量,利用二面角与法向量夹角之间的关系处理,需要注意建系时分析清楚哪三条线互相垂直.
试题解析:
(1)证明:连接![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∵![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ;
;
(2)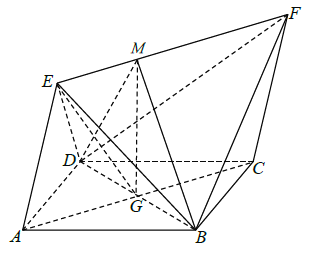
解法一:过![]() 作
作![]() 垂线,垂足为
垂线,垂足为![]() ,连接
,连接![]() ,易得
,易得![]() 为
为![]() 与面
与面![]() 所成的角,
所成的角,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角,
的平面角,
可求得![]() ,
,
在![]() 中由余弦定理可得:
中由余弦定理可得: ![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() ;
;
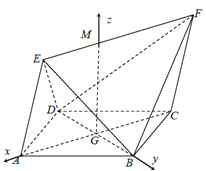
解法二:如图,在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 于
于![]() 点,由(1)可知,平面
点,由(1)可知,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴直线![]() 两两互相垂直,
两两互相垂直,
分别![]() 为
为![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
易得![]() 为
为![]() 与平面
与平面![]() 所成的角,∴
所成的角,∴![]() ,
,
则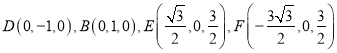 ,
,
 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
![]() 且
且![]() ,
,
∴![]() ,且
,且![]()
取![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
同理可求得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形,  面
面 ,
,  为
为 的中点。
的中点。(1)证明:
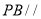 平面
平面 ;
;(2)设
 ,
,  ,三棱锥
,三棱锥 的体积
的体积  ,求A到平面PBC的距离。
,求A到平面PBC的距离。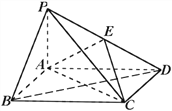
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 为自然对数的底数.
为自然对数的底数.(1)求曲线
 在
在 处的切线方程;
处的切线方程;(2)关于
 的不等式
的不等式 在
在 上恒成立,求实数
上恒成立,求实数 的值;
的值;(3)关于
 的方程
的方程 有两个实根
有两个实根 ,求证:
,求证:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方体ABCD﹣A′B′C′D′中,AB′与A′C′所在直线的夹角为( )
A.30°
B.60°
C.90°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用
 (单位:元)关于月用电量
(单位:元)关于月用电量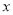 (单位:度)的函数解析式;
(单位:度)的函数解析式;(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求
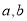 的值;
的值;
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
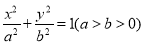 经过点
经过点 ,离心率为
,离心率为 ,动点
,动点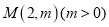 .
.(Ⅰ)求椭圆的标准方程;
(Ⅱ)求以
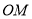 为直径且被直线
为直径且被直线 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;(Ⅲ)设
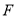 是椭圆的右焦点,过点
是椭圆的右焦点,过点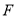 作
作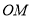 的垂线与以
的垂线与以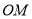 为直径的圆交于点
为直径的圆交于点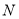 ,证明:线段
,证明:线段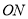 的长为定值,并求出这个定值.
的长为定值,并求出这个定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 (
( )的右焦点为F(2,0),且过点P(2,
)的右焦点为F(2,0),且过点P(2,  ). 直线
). 直线 过点F且交椭圆C于A、B两点.
过点F且交椭圆C于A、B两点.(1)求椭圆C的方程;
(2)若线段AB的垂直平分线与x轴的交点为M(
 ),求直线
),求直线 的方程。
的方程。
相关试题

