【题目】已知函数![]() 为自然对数的底数.
为自然对数的底数.
(1)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的值;
的值;
(3)关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,求证:
,求证: ![]() .
.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ; (3)见解析.
; (3)见解析.
【解析】(1)对函数![]() 求导得
求导得![]() ,
,
∴![]() ,
,
又![]() ,
,
∴曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() ;
;
(2)记![]() ,其中
,其中![]() ,
,
由题意知![]() 在
在![]() 上恒成立,下求函数
上恒成立,下求函数![]() 的最小值,
的最小值,
对![]() 求导得
求导得![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时, ![]() 变化情况列表如下:
变化情况列表如下:
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
∴![]() ,
,
∴![]() ,
,
记![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .
.
当![]() 变化时,
变化时, ![]() 变化情况列表如下:
变化情况列表如下:
|
| 1 |
|
| + | 0 | - |
|
| 极大值 |
|
∴![]() ,
,
故![]() 当且仅当
当且仅当![]() 时取等号,
时取等号,
又![]() ,从而得到
,从而得到![]() ;
;
(3)先证![]() ,
,
记![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,
,
当![]() 变化时,
变化时, ![]() 变化情况列表如下:
变化情况列表如下:
|
|
|
|
| - | 0 | + |
|
| 极小值 |
|
∴![]() ,
,
![]() 恒成立,即
恒成立,即![]() ,
,
记直线![]() 分别与
分别与![]() 交于
交于![]() ,
,
不妨设![]() ,则
,则![]() ,
,
从而![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
由(2)知, ![]() ,则
,则![]() ,
,
从而![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
故![]() ,
,
因等号成立的条件不能同时满足,故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
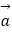 、
、 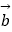 、
、 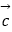 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 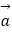 =(1,2).
=(1,2).
(1)若|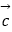 |=2
|=2 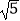 ,且
,且 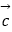 ∥
∥ 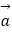 ,求
,求 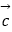 的坐标.
的坐标.
(2)若|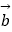 |=
|= 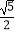 ,且
,且 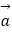 +2
+2 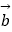 与2
与2 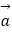 ﹣
﹣ 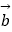 垂直,求
垂直,求 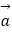 与
与 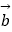 的夹角θ
的夹角θ -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学一位高三班主任对本班50名学生学习积极性和对班级工作的态度进行调查, 得倒的统计数据如表所示:
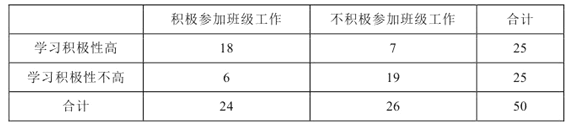
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作的且学习积极性高的7名学生中有两名男生,现从中抽取2名学生参加某项活动,问2名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班级工作的态度是否有关系?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为矩形,
为矩形,  面
面 ,
,  为
为 的中点。
的中点。(1)证明:
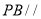 平面
平面 ;
;(2)设
 ,
,  ,三棱锥
,三棱锥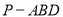 的体积
的体积  ,求A到平面PBC的距离。
,求A到平面PBC的距离。
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体ABCD﹣A′B′C′D′中,AB′与A′C′所在直线的夹角为( )
A.30°
B.60°
C.90°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
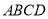 为菱形,四边形
为菱形,四边形 为平行四边形,设
为平行四边形,设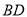 与
与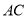 相交于点
相交于点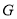 ,
, 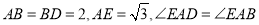 .
.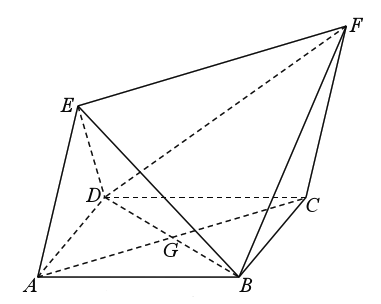
(1)证明:平面
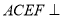 平面
平面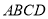 ;
;(2)若
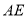 与平面
与平面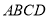 所成角为60°,求二面角
所成角为60°,求二面角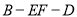 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用
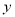 (单位:元)关于月用电量
(单位:元)关于月用电量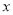 (单位:度)的函数解析式;
(单位:度)的函数解析式;(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求
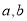 的值;
的值;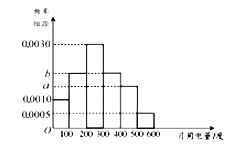
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
相关试题

