【题目】在直三棱柱![]() 中,
中, ![]() ,∠ACB=90°,M是
,∠ACB=90°,M是![]() 的中点,N是
的中点,N是![]() 的中点.
的中点.
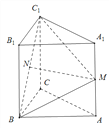
(Ⅰ)求证:MN∥平面![]() ;
;
(Ⅱ)求点![]() 到平面BMC的距离.
到平面BMC的距离.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据图形取B1C1中点D,连结ND、A1D,得到四边形A1MND为平行四边形,从而得到线面平行。(2)先证得BC⊥平面A1MC1,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离,从而得到点面距离。
解析:
(1)如图所示,取B1C1中点D,连结ND、A1D ∴DN∥BB1∥AA1
又DN=![]() ,∴四边形A1MND为平行四边形。
,∴四边形A1MND为平行四边形。
∴MN∥A1 D 又MN ![]() 平面A1B1C1,AD1
平面A1B1C1,AD1![]() 平面A1B1C1 ∴MN∥平面
平面A1B1C1 ∴MN∥平面![]()
(2)因三棱柱![]() 为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2![]() ,CM=C1M=
,CM=C1M=![]() ∴.
∴. ![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业根据供销合同生产某种型号零件10万件,规定:零件长度(单位:毫米)在区间
 内,则为一等品;若长度在
内,则为一等品;若长度在 或
或 内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.
内,则为二等品;否则为不合格产品.现从生产出的零件中随机抽取100件作样本,其长度数据的频率分布直方图如图所示.(1)试估计该样本的平均数;
(2)根据合同,企业生产的每件一等品可获利10元,每件二等品可获利8元,每件不合格产品亏损6元,若用样本估计总体,试估算该企业生产这批零件所获得的利润.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩卡片游戏:他们手里都拿着分别标有数字1,2,3,4,5,6的6张卡片,各自从自己的卡片中随机抽出1张,规定两人谁抽出的卡片上的数字大,谁就获胜,数字相同则为平局.
(1)求甲获胜的概率.
(2)现已知他们都抽出了标有数字6的卡片,为了分出胜负,他们决定从手里剩下的卡片中再各自随机抽出1张,若他们这次抽出的卡片上数字之和为偶数,则甲获胜,否则乙获胜.请问:这个规则公平吗,为什么 ?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
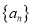 的前
的前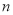 项和为
项和为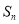 ,
,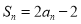 .
.(1)求数列
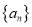 的通项公式;
的通项公式;(2)设
 ,
,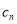 =
=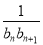 ,记数列
,记数列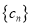 的前
的前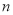 项和
项和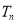 .若对
.若对 ,
, 恒成立,求实数
恒成立,求实数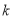 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,且a2=﹣14,a5=﹣5.
(1)求数列{an}的通项an;
(2)求{an}前n项和Sn的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,其中向量
,其中向量  (x∈R),
(x∈R),
(1)求函数y=f(x)的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为a、b、c,已知f (A)=2,a= ,b=
,b=  ,求边长c的值.
,求边长c的值.
相关试题

