【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC= ![]() .
. 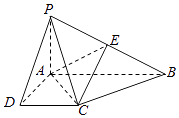
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值.
参考答案:
【答案】
(1)证明:∵AD⊥AB,DC∥AB,∴DC⊥AD,
∵PA⊥平面ABCD,DC平面ABCD,∴DC⊥PA,
∵AD∩PA=A,∴DC⊥平面PAD,
∵DC平面PCD,
∴平面PAD⊥平面PCD
(2)解:作EF⊥AB于F点,

在△ABP中,PA⊥AB,∴EF∥PA,
∴EF⊥平面ABCD,
设EF=h,AD= ![]() =1,
=1, ![]() ,
,
则 ![]() ,
,
![]() =
= ![]() =
= ![]() ,
,
由VPDCEA:VEACB=2:1,得( ![]() ):
): ![]() =2:1,解得h=
=2:1,解得h= ![]() ,
,
EF= ![]() PA,故E为PB的中点
PA,故E为PB的中点
(3)解:连结FC,FD,FD与AC交于点O,连结OE,

由(2)知EF⊥平面ABCD,∴EF⊥AC,
∵ADCF为正方形,∴FO⊥AC,
∵FO∩EF=F,
∴AC⊥平面EFO,∴EO⊥AC,
∴∠EOF是二面角E﹣AC﹣B的平面角,
∵PA⊥平面ABCD,∴平面PAC⊥平面ABCD,
∴二面角E﹣ACB与二面角E﹣AC﹣P互余,
设二面角E﹣AC﹣P的平面角为θ,
则cosθ=sin∠EOF,
在Rt△EOF中,EF= ![]() ,FO=
,FO= ![]() ,EO=
,EO= ![]() ,
,
cosθ=sin ![]() ,
,
∴二面角E﹣AC﹣P的余弦值为 ![]()
【解析】(1)推导出DC⊥AD,DC⊥PA,由此能证明平面PAD⊥平面PCD.(2)作EF⊥AB于F点,则EF⊥平面ABCD,设EF=h,由VPDCEA:VEACB=2:1,解得h= ![]() ,从而得到E为PB的中点.(3)连结FC,FD,FD与AC交于点O,连结OE,推导出EF⊥AC,FO⊥AC,EO⊥AC,从而∠EOF是二面角E﹣AC﹣B的平面角,由二面角E﹣ACB与二面角E﹣AC﹣P互余,能求出二面角E﹣AC﹣P的余弦值.
,从而得到E为PB的中点.(3)连结FC,FD,FD与AC交于点O,连结OE,推导出EF⊥AC,FO⊥AC,EO⊥AC,从而∠EOF是二面角E﹣AC﹣B的平面角,由二面角E﹣ACB与二面角E﹣AC﹣P互余,能求出二面角E﹣AC﹣P的余弦值.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x)满足f(x+1)=
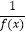 ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
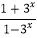 . (Ⅰ)求函数f(x)的定义域和值域;
. (Ⅰ)求函数f(x)的定义域和值域;
(Ⅱ)判断函数f(x)的奇偶性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
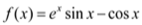 ,
, ,其中
,其中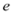 是自然对数的底数.
是自然对数的底数.(Ⅰ)判断函数
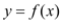 在
在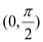 内零点的个数,并说明理由;
内零点的个数,并说明理由;(Ⅱ)
 ,
, ,使得不等式
,使得不等式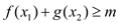 成立,试求实数
成立,试求实数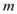 的取值范围;
的取值范围;(Ⅲ)若
 ,求证:
,求证: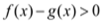 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2
 ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.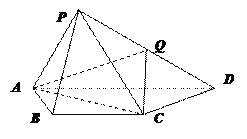
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣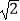 =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2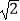 ,求满足条件的实数a的取值.
,求满足条件的实数a的取值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 cosx(sinx+cosx). (Ⅰ)若0<α<
cosx(sinx+cosx). (Ⅰ)若0<α<  ,且sinα=
,且sinα=  ,求f(α)的值;
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
相关试题

