【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)1(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)首先求函数的导数![]() ,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式
,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式![]() 等价于
等价于![]() ,根据导数分别求两个函数的最小值和最大值,建立不等式求
,根据导数分别求两个函数的最小值和最大值,建立不等式求![]() 的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即
的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即![]() ,证明
,证明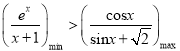 ,求
,求![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]() 在
在![]() 上的零点的个数为1,,
上的零点的个数为1,,
理由如下:因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以函数![]() 在
在![]() 上是单调递增函数.
上是单调递增函数.
因为![]() ,
,![]() ,
,
根据函数零点存在性定理得
函数![]() 在
在![]() 上的零点的个数为1.
上的零点的个数为1.
(Ⅱ)因为不等式![]() 等价于
等价于![]() ,
,
所以![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,等价于
成立,等价于![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 时,
时,![]() 取得最小值-1,
取得最小值-1,
又![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因此,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
只要证![]()
![]() ,
,
只要证![]() ,
,
由于![]() ,
,![]() 只要证
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是单调递减;
是单调递减;
当![]() 时,
时,![]() ,
,![]() 是单调递增.
是单调递增.
所以当且仅当![]() 时,
时,![]() 取得极小值也就是最小值为1.
取得极小值也就是最小值为1.
令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率,
连线的斜率,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
当直线![]() 取得斜率
取得斜率![]() 的最大值为1.
的最大值为1.
故![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
综上所述,当![]() 时,
时,![]() 成立.
成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率.
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x)满足f(x+1)=
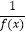 ,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
,且f(x)在[﹣3,﹣2]上是减函数,若α,β是锐角三角形的两个内角,则( )
A.f(sinα)>f(sinβ)
B.f(cosα)>f(cosβ)
C.f(sinα)>f(cosβ)
D.f(sinα)<f(cosβ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
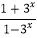 . (Ⅰ)求函数f(x)的定义域和值域;
. (Ⅰ)求函数f(x)的定义域和值域;
(Ⅱ)判断函数f(x)的奇偶性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=
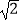 .
. 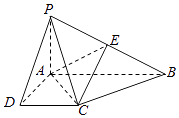
(1)求证:平面PAD⊥平面PCD;
(2)试在棱PB上确定一点E,使截面AEC把该几何体分成的两部分PDCEA与EACB的体积比为2:1;
(3)在(2)的条件下,求二面角E﹣AC﹣P的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,PA=AB=BC=CD=2,PD=2
 ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.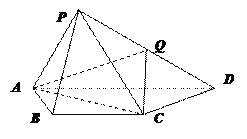
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求直线PD与平面AQC所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知动点P(x,y)满足方程xy=1(x>0).
(Ⅰ)求动点P到直线l:x+2y﹣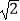 =0距离的最小值;
=0距离的最小值;
(Ⅱ)设定点A(a,a),若点P,A之间的最短距离为2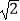 ,求满足条件的实数a的取值.
,求满足条件的实数a的取值.
相关试题

