【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC. 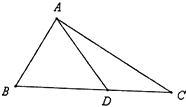
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ![]() ,求DC的长.
,求DC的长.
参考答案:
【答案】解:(Ⅰ)在△ABC中,根据正弦定理,有 ![]() =
= ![]() . ∵AC=
. ∵AC= ![]() DC,∴sin∠ADC=
DC,∴sin∠ADC= ![]() =
= ![]() .
.
又∠ADC=∠B+∠BAD=∠B+60°>60° ,
∴∠ADC=120°.
于是∠C=180°﹣120°﹣30°=30° , ∴∠B=60°.
(Ⅱ)设DC=x,则BD=2x,BC=3x,AC= ![]() x.
x.
于是sinB= ![]() =
= ![]() ,cosB=
,cosB= ![]() ,AB=
,AB= ![]() x.
x.
在△ABD中,由余弦定理,AD2=AB2+BD2﹣2ABBDcosB,
即 ![]() ,得x=1.故DC=1
,得x=1.故DC=1
【解析】(Ⅰ)利用正弦定理、外角性质、三角形内角和定理即可得出.(Ⅱ)设DC=x,则BD=2x,BC=3x,AC= ![]() x.于是sinB=
x.于是sinB= ![]() =
= ![]() ,cosB=
,cosB= ![]() ,AB=
,AB= ![]() x.再利用余弦定理即可得出.
x.再利用余弦定理即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数F(x)=
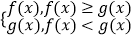 ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=
 (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
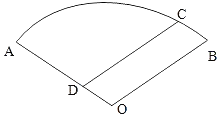
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示.
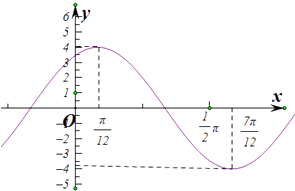
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于平面向量,有下列四个命题:
①若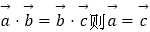 .
.
②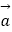 =(1,1),
=(1,1), 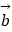 =(2,x),若
=(2,x),若 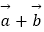 与
与 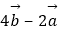 平行,则x=2.
平行,则x=2.
③非零向量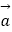 和
和 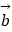 满足|
满足| 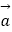 |=|
|=| 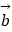 |=|
|=| 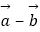 |,则
|,则 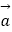 与
与 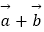 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量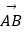 同方向的单位向量为(
同方向的单位向量为( 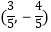 ).
).
其中真命题的序号为 . (写出所有真命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
相关试题

