【题目】设函数F(x)= ![]() ,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
,其中f(x)=log2(x2+1),g(x)=log2(|x|+7).
(1)在实数集R上用分段函数形式写出函数F(x)的解析式;
(2)求函数F(x)的最小值.
参考答案:
【答案】
(1)
解:F(x)= 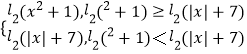 ,
,
令log2(x2+1)≥log2(|x|+7),得x2﹣|x|﹣6≥0,
解得:x≤﹣3或x≥3,(5分)∴F(x)= 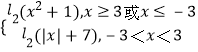
(2)
解:当x≥3或x≤﹣3时,F(x)=log2(x2+1),设u=x2+1≥10,y=log2u在[10,+∞)上递增,所以F(x)min=log210;(说明:设元及单调性省略不扣分)
同理,当﹣3<x<3,F(x)min=log27;
又log27<log210∴x∈R时,F(x)min=log27.
或解:因为F(x)是偶函数,所以只需要考虑x≥0的情形,
当0≤x<3,F(x)=log2(x2+7),当x=0时,F(x)min=log27;
当x≥3时,F(x)=log2(x2+1),当x=3时,F(x)min=log210;
∴x∈R时,F(x)min=log27
【解析】(1)令log2(x2+1)≥log2(|x|+7),解得:x的取值范围,再结合F(x)的意义用分段函数形式写出函数F(x)的解析式即可;(2)先分情况讨论函数的单调性:当x≥3或x≤﹣3时;当﹣3<x<3,分别求出F(x)的最小值,最后综合得出x∈R时,F(x)min=log27.或利用F(x)的奇偶性,只需要考虑x≥0的情形,只须分两种情形讨论:当0≤x<3,当x≥3时,分别求得F(x)的最小值即得.
【考点精析】关于本题考查的函数的值域,需要了解求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
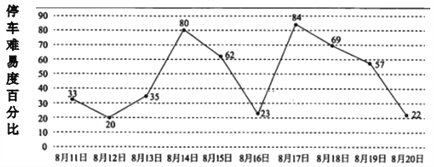
(Ⅰ)求小辉连续两天都遇上停车场较难的概率;
(Ⅱ)设
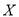 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求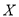 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
-
科目: 来源: 题型:
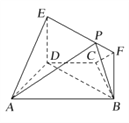
查看答案和解析>>【题目】如图,在梯形
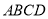 中,
中, 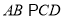 ,
, 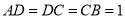 ,
, 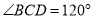 ,四边形
,四边形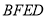 为矩形,平面
为矩形,平面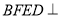 平面
平面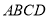 ,
, 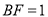 .
.
(Ⅰ)求证:
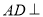 平面
平面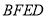 ;
;(Ⅱ)点
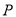 在线段
在线段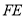 上运动,设平面
上运动,设平面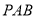 与平面
与平面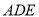 所成锐二面角为
所成锐二面角为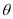 ,试求
,试求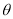 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某早餐店每天制作甲、乙两种口味的糕点共n(nN*)份,每份糕点的成本1元,售价2元,如果当天卖不完,剩下的糕点作废品处理.该早餐店发现这两种糕点每天都有剩余,为此整理了过往100天这两种糕点的日销量(单位:份),得到如下的统计数据:
甲口味糕点日销量
48
49
50
51
天数
20
40
20
20
乙口味糕点日销量
48
49
50
51
天数
40
30
20
10
以这100天记录的各销量的频率作为各销量的概率,假设这两种糕点的日销量相互独立.
(1)记该店这两种糕点每日的总销量为X份,求X的分布列
(2)早餐店为了减少浪费,提升利润,决定调整每天制作糕点的份数
①若产生浪费的概率不超过0.6,求n的最大值;
②以销售这两种糕点的日总利润的期望值为决策依据,在每天所制糕点能全部卖完与n=98之中选其一,应选哪个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=
 (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积 -
科目: 来源: 题型:
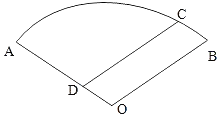
查看答案和解析>>【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是直角△ABC斜边BC上一点,AC=
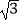 DC.
DC. 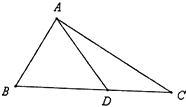
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ,求DC的长.
,求DC的长.
相关试题

