【题目】已知定义在R上的函数f(x)=Asin(ωx+φ)(x>0,A>0)的图象如图所示. 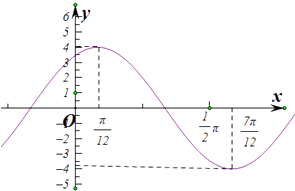
(1)求函数f(x)的解析式;
(2)写出函数f(x)的单调递增区间
(3)设不相等的实数,x1 , x2∈(0,π),且f(x1)=f(x2)=﹣2,求x1+x2的值.
参考答案:
【答案】
(1)解:由函数f(x)的图象可得A=4,
又∵函数的周期T=2( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω═ ![]() =2,
=2,
∵函数图象经过点P( ![]() ,4),即:4sin(2×
,4),即:4sin(2× ![]() +φ)=4,
+φ)=4,
∴利用五点作图法可得:2× ![]() +φ=
+φ= ![]() ,求得:φ=
,求得:φ= ![]() ,
,
∴函数的表达式为: ![]()
(2)解:由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可得:kπ﹣
,k∈Z,可得:kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,k∈Z,
,k∈Z,
可得函数f(x)的单调递增区间为: ![]()
(3)解:∵x∈(0,π),
∴2x+ ![]() ∈(
∈( ![]() ,
, ![]() ),
),
又∵f(x)=﹣2,可得:sin(2x+ ![]() )=﹣
)=﹣ ![]() ,
,
∴2x+ ![]() =
= ![]() 或
或 ![]() ,解得:x=
,解得:x= ![]() 或
或 ![]() ,
,
∴x1+x2= ![]()
【解析】(1)根据函数的最值得到A,再由函数的周期为2( ![]() ﹣
﹣ ![]() )=π,结合周期公式得到ω的值,再根据函数的最大值对应的x值,代入并解之得φ,从而得到函数的表达式.(2)由2kπ﹣
)=π,结合周期公式得到ω的值,再根据函数的最大值对应的x值,代入并解之得φ,从而得到函数的表达式.(2)由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,k∈Z,可解得f(x)的单调递增区间.(3)由题意可得2x+
,k∈Z,可解得f(x)的单调递增区间.(3)由题意可得2x+ ![]() ∈(
∈( ![]() ,
, ![]() ),又f(x)=﹣2,可得:sin(2x+
),又f(x)=﹣2,可得:sin(2x+ ![]() )=﹣
)=﹣ ![]() ,进而解得符合条件的不相等的2个实数解,即可得解.
,进而解得符合条件的不相等的2个实数解,即可得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
点P是曲线C1:(x-2)2+y2=4上的动点,以坐标原点O为极点,x轴的正半轴为极轴
建立极坐标系,将点P绕极点O逆时针90得到点Q,设点Q的轨迹为曲线C2.
求曲线C1,C2的极坐标方程;
射线=
 (>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积
(>0)与曲线C1,C2分别交于A,B两点,定点M(2,0),求MAB的面积 -
科目: 来源: 题型:
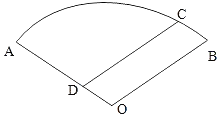
查看答案和解析>>【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D是直角△ABC斜边BC上一点,AC=
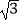 DC.
DC. 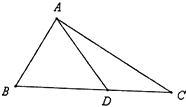
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ,求DC的长.
,求DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】关于平面向量,有下列四个命题:
①若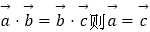 .
.
②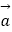 =(1,1),
=(1,1), 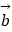 =(2,x),若
=(2,x),若 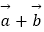 与
与 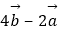 平行,则x=2.
平行,则x=2.
③非零向量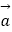 和
和 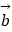 满足|
满足| 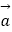 |=|
|=| 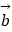 |=|
|=| 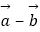 |,则
|,则 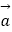 与
与 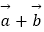 的夹角为60°.
的夹角为60°.
④点A(1,3),B(4,﹣1),与向量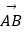 同方向的单位向量为(
同方向的单位向量为( 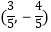 ).
).
其中真命题的序号为 . (写出所有真命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x-3)ex+ax,aR
(1)当a=1时,求曲线f(x)在点(2,f(2))处的切线方程;
(2)当a[0,e)时,设函数f(x)在(1,+)上的最小值为g(a),求函数g(a)的值域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明与化简.
(1)求证:cotα=tanα+2cot2α;
(2)请利用(1)的结论证明:cotα=tanα+2tan2α+4cot4α;
(3)请你把(2)的结论推到更一般的情形,使之成为推广后的特例,并加以证明:
(4)化简:tan5°+2tan10°+4tan20°+8tan50°.
相关试题

