【题目】已知椭圆![]()
![]() 的右顶点
的右顶点![]() ,离心率为
,离心率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
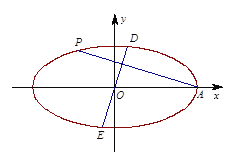
(Ⅱ)已知![]() (异于点
(异于点![]() )为椭圆
)为椭圆![]() 上一个动点,过
上一个动点,过![]() 作线段
作线段![]() 的垂线
的垂线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ) ![]() .
.
【解析】
(1)由椭圆右顶点求出![]() ,由离心率求出
,由离心率求出![]() ,再由
,再由![]() 求出
求出![]() ,从而求出椭圆方程;(2)先考虑AP斜率不存在,再考虑斜率存在时,设出AP方程,联立椭圆方程,解出点P坐标,然后求出AP长度,同理求出DE长度,从而求出
,从而求出椭圆方程;(2)先考虑AP斜率不存在,再考虑斜率存在时,设出AP方程,联立椭圆方程,解出点P坐标,然后求出AP长度,同理求出DE长度,从而求出![]() 比值,用换元法结合单调性求出其范围.
比值,用换元法结合单调性求出其范围.
解:(Ⅰ)因为![]() 是椭圆
是椭圆![]() 的右顶点,所以
的右顶点,所以![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]() .
.
所以椭圆![]() 的方程为
的方程为![]()
(Ⅱ)当直线![]() 的斜率为0时,
的斜率为0时,![]() ,
,![]() 为椭圆
为椭圆![]() 的短轴,
的短轴,
则![]() ,所以
,所以![]() .
.
当直线![]() 的斜率不为0时,
的斜率不为0时,
设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
则直线DE的方程为![]() .
.
由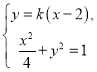
得![]() .
.
所以![]()
所以![]()
所以![]() ..
..
同理可求![]() .
.
所以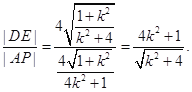
设![]() 则
则![]() ,
,![]() .
.
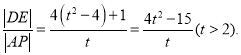
令![]() ,
,
则![]() .
.
所以![]() 是一个增函数.
是一个增函数.
所以![]() .
.
综上:![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+
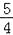 }是等比数列.
}是等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形
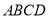 ,
,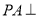 面
面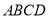 ,
,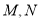 分别是
分别是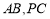 的中点,设
的中点,设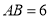 ,
,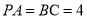 .
.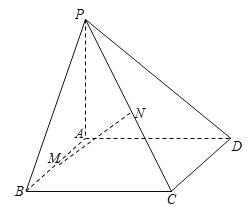
(1)证明:
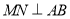 ;
;(2)求二面角
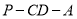 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】给定公差大于0的有限正整数等差数列
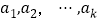 ,其中,
,其中,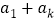 为质数.甲、乙两人轮流从
为质数.甲、乙两人轮流从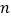 个石子中取石子,规定:每次每人可取
个石子中取石子,规定:每次每人可取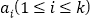 个石子,取走的石子不再放回,甲先取,取到最后一个石子者为胜.试问:谁有必胜策略?
个石子,取走的石子不再放回,甲先取,取到最后一个石子者为胜.试问:谁有必胜策略? -
科目: 来源: 题型:
查看答案和解析>>【题目】以
 为直径的圆上每一点都染上了红、黄、蓝三色之一,已知
为直径的圆上每一点都染上了红、黄、蓝三色之一,已知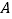 、
、 染上了红色,联结圆上的点组成三角形,给出4个结论:
染上了红色,联结圆上的点组成三角形,给出4个结论:①必定存在一个直角三角形,三个顶点同为红色;
②必定存在一个直角三角形,三个顶点同色;
③必定存在一个直角三角形,三个顶点全不同色;
④必定存在一个直角三角形,或都三个顶点同色,或者三个顶点全不同色。
则真命题的个数是( )个。
A. 1 B. 2
C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一道题目的证明,指出其中的一处错误。题目:平面上有六个点,任何三点都是三边互不相等三角形的顶点,则这些三角形中有一个的最短边又是另一个三角形的最长边。证明:第一步,对已知的六个点作两两连线,可以得出15条边,记为
 ,
, ,…,
,…, .第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设
.第二步,由于任何三点组成的都是“三边互不相等的三角形”,因此,15条边互不相等不妨设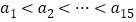 .第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则
.第三步,由于“任何三点都是三边互不相等三角形的顶点”,因此,任取三条边都可以组成三角形,则 、
、 、
、 组成的三角形的最长边
组成的三角形的最长边 ,也是
,也是 、
、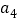 、
、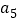 组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______.
组成的三角形的最短边,命题得证.这三步中,第______步有错误,理由是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的类比过程。
(1)在一维直线上,线段是一个封闭的中心对称图形,有命题1:不重合的两点决定一条线段;
(2)在二维平面上,圆是一个封闭的中心对称图形,有命题2:不共线的三点决定一个圆;
(3)在三维空间中,球是一个封闭的中心对称图形,类比猜想:不共面的四点决定一个球。
证明或否定这个类比猜想:不共面的四点决定一个球。
相关试题

