【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点. 
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值.
参考答案:
【答案】
(1)证明:∵F、G分别是AC、BC中点.
∴FG∥AB,
∵FG平面ABE,AB平面ABE,
∴FG∥平面ABE,
∵DE∥BC,BC=2DE,G是BC中点,
∴DE ![]() BG,∴四边形DEBG是平行四边形,
BG,∴四边形DEBG是平行四边形,
∴DG∥BE,
∵DG平面ABE,BE平面ABE,
∴DG∥平面ABE,
∵DG∩FG=G,DG,FG平面DFG,
AB∩BE=B,AB,BE平面ABE,
∴平面DFG∥平面ABE
(2)解:∵DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
∴以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,
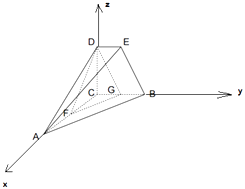
∵AC=2BC=2CD=4,
∴A(4,0,0),B(0,2,0),C(0,0,2),E(0,1,2),
![]() =(﹣4,1,2),
=(﹣4,1,2), ![]() =(﹣4,2,0),
=(﹣4,2,0), ![]() =(﹣4,0,2),
=(﹣4,0,2),
设平面ABE的法向量 ![]() =(x,y,z),
=(x,y,z),
则 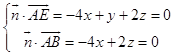 ,取x=1,得
,取x=1,得 ![]() =(1,0,2),
=(1,0,2),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
则cos< ![]() >=
>= ![]() .
.
∴二面角E﹣AB﹣C的余弦值为cosα= ![]() ,
,
则sinα= ![]() ,tanα=
,tanα= ![]() =
= ![]() .
.
∴二面角E﹣AB﹣C的正切值为 ![]() .
.
【解析】(1)推导出FG∥AB,从而FG∥平面ABE,从而出四边形DEBG是平行四边形,从而DG∥BE,进而DG∥平面ABE,由此能证明平面DFG∥平面ABE.(2)以C为原点,CA为x轴,以CB为y轴,以CD为z轴,建立空间直角坐标系,利用向量法能求出二面角E﹣AB﹣C的正切值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2 , 若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
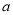 为何值时,
为何值时, 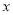 轴为曲线
轴为曲线 的切线;
的切线;(2)用
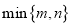 表示
表示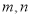 中的最小值,设函数
中的最小值,设函数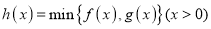 ,讨论
,讨论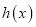 零点的个数.
零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的奇函数f(x)=
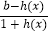 ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差d>0的等差数列{an}中,a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求公差d及通项an;
(2)设Sn= +
+  +…+
+…+  ,求证:Sn<
,求证:Sn<  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义函数序列:
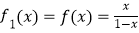 ,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线
,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线 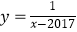 的交点坐标为( )
的交点坐标为( )
A.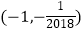
B.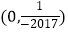
C.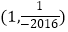
D.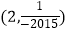
相关试题

