【题目】已知公差d>0的等差数列{an}中,a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求公差d及通项an;
(2)设Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,求证:Sn<
,求证:Sn< ![]() .
.
参考答案:
【答案】
(1)解:∵a1,2a2+2,5a3成等比数列,∴ ![]() =a15a3,∴(2×10+2d+2)2=10×5(10+2d),
=a15a3,∴(2×10+2d+2)2=10×5(10+2d),
化为:d2﹣3d﹣4=0,d>0,解得d=4.∴an=10+4(n﹣1)=4n+6
(2)证明: ![]() =
= ![]() =
= ![]()
![]() .
.
∴Sn= ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]()
![]() +
+ ![]() +…+
+…+ ![]()
= ![]()
![]() <
< ![]() ﹣
﹣ ![]() <
< ![]()
【解析】(1)由a1 , 2a2+2,5a3成等比数列,可得 ![]() =a15a3 , 即(2×10+2d+2)2=10×5(10+2d),化为:d2﹣3d﹣4=0,d>0,解得d即可得出.(2)
=a15a3 , 即(2×10+2d+2)2=10×5(10+2d),化为:d2﹣3d﹣4=0,d>0,解得d即可得出.(2) ![]() =
= ![]() =
= ![]()
![]() .利用“裂项求和方法”即可得出.
.利用“裂项求和方法”即可得出.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系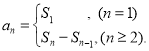 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
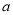 为何值时,
为何值时, 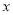 轴为曲线
轴为曲线 的切线;
的切线;(2)用
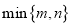 表示
表示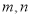 中的最小值,设函数
中的最小值,设函数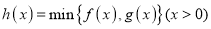 ,讨论
,讨论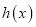 零点的个数.
零点的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义域为R的奇函数f(x)=
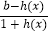 ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.

(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E﹣AB﹣C的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=loga(ax+1)+mx是偶函数.
(1)求m;
(2)当a>1时,若函数f(x)的图像与直线l:y=﹣mx+n无公共点,求n的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义函数序列:
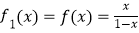 ,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线
,f2(x)=f(f1(x)),f3(x)=f(f2(x)),…,fn(x)=f(fn﹣1(x)),则函数y=f2017(x)的图像与曲线 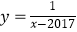 的交点坐标为( )
的交点坐标为( )
A.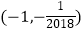
B.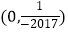
C.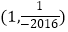
D.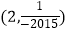
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中 ①若loga3>logb3,则a>b;
②函数f(x)=x2﹣2x+3,x∈[0,+∞)的值域为[2,+∞);
③设g(x)是定义在区间[a,b]上的连续函数.若g(a)=g(b)>0,则函数g(x)无零点;
④函数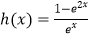 既是奇函数又是减函数.
既是奇函数又是减函数.
其中正确的命题有
相关试题

