【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
加工时间
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(1)画出散点图,并判断![]() 与
与![]() 是否具有线性相关关系;
是否具有线性相关关系;

(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
, ![]() .
.
参考数据 | 合计 | ||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 550 |
| 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 | 917 |
| 100 | 400 | 900 | 1600 | 2500 | 3600 | 4900 | 6400 | 8100 | 10000 | 38500 |
| 620 | 1360 | 2250 | 3240 | 4450 | 5700 | 7140 | 8840 | 10350 | 12200 | 55950 |
参考答案:
【答案】(1)见解析;(2)![]() ;(3)加工2010个拼图所需时间约为23.3小时.
;(3)加工2010个拼图所需时间约为23.3小时.
【解析】试题分析:(1)根据表中数据,画出散点图,
由散点图成带状分布,得出两个变量具有线性相关关系;
(2)计算![]() ,求出回归系数
,求出回归系数![]() ,写出回归方程;
,写出回归方程;
(3)计算x=200时![]() 的值即可.
的值即可.
试题解析:
(1)散点图如图所示,
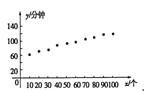
由散点图可以看出,两个变量具有线性相关关系.
(2)经计算得![]() ,
, ![]() ,求和
,求和![]() ,求和
,求和![]() ,
,
设所求的回归方程为![]() ,则有
,则有![]() ,
, ![]() ,
,
因此,所求的回归方程是![]() .
.
(3)当![]() 时,
时, ![]() (分钟),
(分钟),![]() ,
,
因此,加工2010个拼图所需时间约为23.3小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:-1≤x<2,q:x<a,若q是p的必要条件,则a的取值范围是( )
A.a≤-1B.a≤-1或a≥2C.a≥2D.-1≤a<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
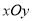 中,点
中,点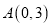 ,直线
,直线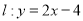 .设圆
.设圆 的半径为1,圆心在
的半径为1,圆心在 上.
上.(1)若圆心
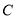 也在直线
也在直线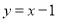 上,过点
上,过点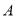 作圆
作圆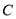 的切线,求切线的方程;
的切线,求切线的方程;(2)若圆
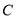 上存在点
上存在点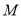 ,使
,使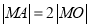 ,求圆心
,求圆心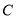 的横坐标
的横坐标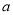 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
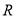 上的函数
上的函数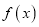 的导函数为
的导函数为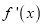 ,且满足
,且满足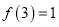 ,
, 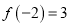 ,当
,当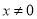 时有
时有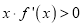 恒成立,若非负实数
恒成立,若非负实数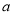 、
、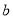 满足
满足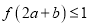 ,
, 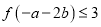 ,则
,则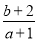 的取值范围为 .
的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设
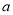 为非负实数,函数
为非负实数,函数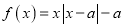 .
.(1)当
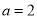 时,求
时,求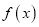 的单调区间;
的单调区间;(2)讨论函数
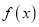 零点的个数,并求出零点.
零点的个数,并求出零点.
相关试题

