【题目】设![]()
![]() 为实数,且
为实数,且![]() ,
,
(I)求方程![]() 的解;
的解;
(II)若![]() 满足
满足![]() ,求证:①
,求证:①![]() ②
②![]() ;
;
(III)在(2)的条件下,求证:由关系式![]() 所得到的关于
所得到的关于![]() 的方程
的方程![]() 存在
存在![]() ,使
,使![]()
参考答案:
【答案】(Ⅰ)![]() 或
或![]() ; (Ⅱ)见解析;(Ⅲ)见解析 .
; (Ⅱ)见解析;(Ⅲ)见解析 .
【解析】
(I)由f(x)=1,得lnx=±1,即可求方程f(x)=1的解;
(II)①证明ln(ab)=0即可;②令![]() ,(b∈(1,+∞)),证明(b)
,(b∈(1,+∞)),证明(b)
在(1,+∞)上为增函数,即可证明结论;
(III)令h(b)=![]() ,因为h(3)<0,h(4)>0,即可得出结论.
,因为h(3)<0,h(4)>0,即可得出结论.
(I)由![]() ,得
,得![]() 所以
所以![]() 或
或![]() 。
。
(II)证明:①因为![]() ,且
,且![]() ,可判断
,可判断![]() ,
,![]()
所以![]() ,即
,即![]() 即
即![]() ,则
,则![]()
②由①得![]() 令
令![]() ,(
,(![]() )
)
任取![]() 且
且![]()
因为![]()
![]()
![]()
=![]() =
=![]() =
=![]()
![]()
![]()
![]()
![]() ,
,
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,
,![]() .
.
(III)证明:![]()
![]()
![]()
![]() ,得
,得![]() 又
又![]()
![]()
令![]()
![]() ,因为
,因为![]()
根据函数零点的判断条件可知,函数![]() 在(3,4)内一定存在零点,
在(3,4)内一定存在零点,
即存在![]() 使
使![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据市场分析,某蔬菜加工点,当月产量为10吨至25吨时,月生产总成本
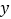 (万元)可以看出月产量
(万元)可以看出月产量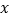 (吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.
(吨)的二次函数,当月产量为10吨时,月生产成本为20万元,当月产量为15吨时,月生产总成本最低至17.5万元.(I)写出月生产总成本
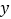 (万元)关于月产量
(万元)关于月产量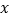 吨的函数关系;
吨的函数关系;(II)已知该产品销售价为每吨1.6万元,那么月产量为多少吨时,可获得最大利润,并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (a为常数)的图象与
(a为常数)的图象与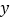 轴交于点
轴交于点 ,曲线
,曲线 在点
在点 处的切线斜率为
处的切线斜率为
(1)求
 的值及函数
的值及函数 的极值;
的极值;(2)证明:当
 时,
时,
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知过抛物线
 的焦点,斜率为
的焦点,斜率为 的直线交抛物线于
的直线交抛物线于 两点,且
两点,且 .
.(1)求该抛物线的方程;
(2)
 为坐标原点,
为坐标原点, 为抛物线上一点,若
为抛物线上一点,若 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x,g(x)是一次函数,并且点(2,2)在函数f[(g(x)]的图象上,点(2,5)在函数g[f(x)]的图象上,则g(x)的解析式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图给出了一个程序框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等,则这样的x值有( )
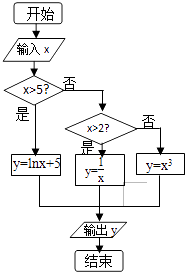
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】设P(x0,y0)是函数f(x)图象上任意一点,且y02≥x02,则f(x)的解析式可以是_____.(填序号)
①f(x)=x﹣
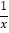 ②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+
②f(x)=ex﹣1(e≈2.718,是一个重要常数)③f(x)=x+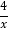 ④y=x2
④y=x2
相关试题

