【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)经过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,记
的左、右顶点,记![]() 与
与![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析: (1)由离心率的值以及点P坐标求出椭圆方程;(2) 当直线![]() 无斜率时,直线方程为
无斜率时,直线方程为![]() ,不合题意; 当直线
,不合题意; 当直线![]() 斜率存在(显然
斜率存在(显然![]() )时,设直线方程为
)时,设直线方程为![]() ,设
,设![]() ,联立直线和椭圆方程,消去y得出关于x的一元二次方程,将韦达定理代入
,联立直线和椭圆方程,消去y得出关于x的一元二次方程,将韦达定理代入![]() ,再根据基本不等式求出最值.
,再根据基本不等式求出最值.
试题解析:(1)因为![]() ,过点
,过点![]() ,
,![]() 所以
所以![]() . 所以椭圆方程为
. 所以椭圆方程为![]()
(2)当直线![]() 无斜率时,直线方程为
无斜率时,直线方程为![]() ,
,
此时![]() ,
, ![]() 面积相等,
面积相等,![]()
当直线![]() 斜率存在(显然
斜率存在(显然![]() )时,设直线方程为
)时,设直线方程为![]() ,
,
设![]()
和椭圆方程联立得到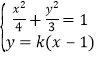 ,消掉
,消掉![]() 得
得![]()
![]()
显然![]() ,方程有根,且
,方程有根,且![]()
此时![]() =
=![]()
因为![]() ,上式
,上式![]() ,(
,(![]() 时等号成立)
时等号成立)
所以![]() 的最大值为
的最大值为![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某三棱锥的三视图如图所示,则三棱锥的体积为( )

A. 10 B. 20 C. 30 D. 60
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,底面
 是边长为3的正方形,
是边长为3的正方形, 平面
平面 ,
, ,
, ,
, 与平面
与平面 所成的角为
所成的角为 .
.
(1)求证:平面
 平面
平面 ;
;(2)求二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
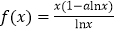 .
.(1)若
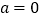 ,求函数在
,求函数在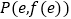 的切线方程;
的切线方程;(2)若函数
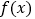 在
在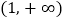 上为单调递减函数,求实数
上为单调递减函数,求实数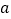 的最小值;
的最小值;(3)若存在
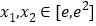 ,使得
,使得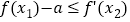 成立,求实数
成立,求实数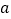 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知极坐标系的极点在平面直角坐标系的原点
 处,极轴与
处,极轴与 轴的非负半轴重合,且长度单位相同,直线
轴的非负半轴重合,且长度单位相同,直线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 (
( 为参数).其中
为参数).其中 .
.(1)试写出直线
 的直角坐标方程及曲线
的直角坐标方程及曲线 的普通方程;
的普通方程;(2)若点
 为曲线
为曲线 上的动点,求点
上的动点,求点 到直线
到直线 距离的最大值.
距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

相关试题

