【题目】已知点m是直线l: ![]() x﹣y+3=0与x轴的交点,将直线l绕点m旋转30°,求所得到的直线l′的方程.
x﹣y+3=0与x轴的交点,将直线l绕点m旋转30°,求所得到的直线l′的方程.
参考答案:
【答案】解:在方程 ![]() x﹣y+3=0中,取y=0,得x=﹣
x﹣y+3=0中,取y=0,得x=﹣ ![]() .
.
∴M( ![]() ),
),
直线 ![]() x﹣y+3=0的斜率为
x﹣y+3=0的斜率为 ![]() ,则其倾斜角为60°,
,则其倾斜角为60°,
直线l绕点M旋转30°,若是逆时针,则直线l′的倾斜角为90°,
∴直线l′的方程为x=﹣ ![]() ;
;
若是顺时针,则直线l′的倾斜角为30°,
∴直线l′的斜率为 ![]() ,
,
∴直线l′的方程为y﹣0= ![]() (x+
(x+ ![]() ),即x﹣
),即x﹣ ![]()
【解析】求出直线l与x轴的交点M的坐标,然后分l顺时针和逆时针旋转求出直线l的倾斜角,再进一步分析斜率的情况,斜率不存在时直接写出直线方程,斜率存在时由直线方程的点斜式求得直线方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
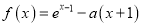 ,
, 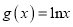 .
.(1)求
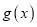 在点
在点 处的切线;
处的切线;(2)讨论
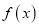 的单调性;
的单调性;(3)当
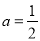 ,
, 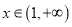 时,求证:
时,求证: 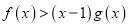 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
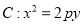 (
(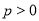 ),过其焦点
),过其焦点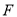 作斜率为1的直线交抛物线
作斜率为1的直线交抛物线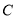 于
于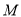 ,
, 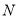 两点,且
两点,且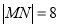 ,
,(1)求抛物线
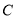 的方程;
的方程;(2)已知动点
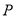 的圆心在抛物线
的圆心在抛物线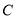 上,且过点
上,且过点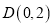 ,若动圆
,若动圆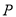 与
与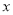 轴交于
轴交于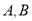 两点,且
两点,且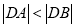 ,求
,求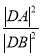 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a3=3,a5+a7=12,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】王府井百货分店今年春节期间,消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对春节前7天参加抽奖活动的人数进行统计,
 表示第
表示第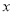 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
1
2
3
4
5
6
7

5
8
8
10
14
15
17
经过进一步统计分析,发现
 与
与 具有线性相关关系.
具有线性相关关系.(1)请根据上表提供的数据,用最小二乘法求出
 关于
关于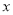 的线性回归方程
的线性回归方程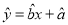 ;
;(2)判断变量
 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;(3)若该活动只持续10天,估计共有多少名顾客参加抽奖.
参与公式:
 ,
, 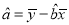 ,
,  .
. -
科目: 来源: 题型:
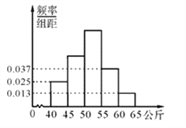
查看答案和解析>>【题目】人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
(Ⅰ)求该校抽取的学生总数以及第2组的频率;
(Ⅱ)学校为进一步了解学生的身体素质,在第1组、第2组、第3组中用分层抽样的方法抽取6人进行测试.若从这6人中随机选取2人去共同完成某项任务,求这2人来自于同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
相关试题

