【题目】在△ABC中,a、b、c分别是角A、B、C的对边,且 ![]() ,
,
(1)求角B的大小;
(2)若 ![]() ,求△ABC的面积.
,求△ABC的面积.
参考答案:
【答案】
(1)解:由正弦定理 ![]() 得:
得:
a=2RsinA,b=2RsinB,c=2RsinC,
将上式代入已知 ![]() ,
,
即2sinAcosB+sinCcosB+cosCsinB=0,
即2sinAcosB+sin(B+C)=0,
∵A+B+C=π,
∴sin(B+C)=sinA,
∴2sinAcosB+sinA=0,即sinA(2cosB+1)=0,
∵sinA≠0,∴ ![]() ,
,
∵B为三角形的内角,∴ ![]() ;
;
(2)解:将 ![]() 代入余弦定理b2=a2+c2﹣2accosB得:
代入余弦定理b2=a2+c2﹣2accosB得:
b2=(a+c)2﹣2ac﹣2accosB,即 ![]() ,
,
∴ac=3,
∴ ![]()
【解析】(1)根据正弦定理表示出a,b及c,代入已知的等式,利用两角和的正弦函数公式及诱导公式变形后,根据sinA不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可求出角B的度数;(2)由(1)中得到角B的度数求出sinB和cosB的值,根据余弦定理表示出b2,利用完全平方公式变形后,将b,a+c及cosB的值代入求出ac的值,然后利用三角形的面积公式表示出△ABC的面积,把ac与sinB的值代入即可求出值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设点Pi(xi , yi)在直线li:aix+biy=ci上,若ai+bi=ici(i=1,2),且|P1P2|≥
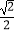 恒成立,则
恒成立,则  +
+  = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和为Sn , 满足3an﹣2Sn﹣1=0.
(1)求数列{an}的通项公式;
(2)bn= ,数列{bn}的前n项和为Tn , 求f(n)=
,数列{bn}的前n项和为Tn , 求f(n)=  (n∈N+)的最大值.
(n∈N+)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(2,﹣1).
(Ⅰ)求过P点且与原点距离为2的直线l的方程;
(Ⅱ)求过P点且与两坐标轴截距相等的直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
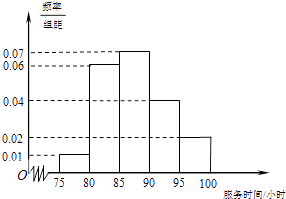
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣4x﹣16,
(1)求不等式g(x)<0的解集;
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方体ABCD﹣A1B1C1D1中,AB=2BB1=2BC,E为D1C1的中点,连结ED,EC,EB和DB.
(Ⅰ)证明:A1D1∥平面EBC;
(Ⅱ)证明:平面EDB⊥平面EBC.
相关试题

