【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
, ![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
, ![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)将基本事件一一列出来,找到满足![]() 的事件,利用古典概型概率公式求概率即可;
的事件,利用古典概型概率公式求概率即可;
(2)将基本事件一一列出来,找到三条线段能围成等腰三角形的事件,利用古典概型概率公式求概率即可.
试题解析:
先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
, ![]() 包含的基本事件有:
包含的基本事件有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() ,共36个.
,共36个.
(1)∵直线![]() 与圆
与圆![]() 相切,
相切,
∴![]() ,整理得:
,整理得: ![]() .
.
由于![]() ,
, ![]() ,
,
∴满足条件的情况只有![]() ,
, ![]() ,或
,或![]() ,
, ![]() 两种情况.
两种情况.
∴直线![]() 与圆
与圆![]() 相切的概率是
相切的概率是![]() .
.
(2)∵三角形的一边长为5,三条线段围成等腰三角形,
∴当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共1个基本事件;
,共1个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
当![]() 时,
时, ![]() ,共6个基本事件;
,共6个基本事件;
当![]() 时,
时, ![]() ,共2个基本事件;
,共2个基本事件;
∴三条线段能围成等腰三角形的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某运动员每次投篮命中的概率等于40%.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下2-组随机数:
907 966 191 925 271 932 812 458
569 683 431 257 393 027 556 488
730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
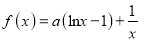 的图象与
的图象与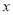 轴相切,
轴相切, 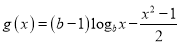 .
.(Ⅰ)求证:
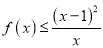 ;
;(Ⅱ)若
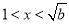 ,求证:
,求证: 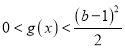
-
科目: 来源: 题型:
查看答案和解析>>【题目】某仪器经过检验合格才能出厂,初检合格率为
 :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为 .每台仪器各项费用如表:
.每台仪器各项费用如表:项目
生产成本
检验费/次
调试费
出厂价
金额(元)
1000
100
200
3000
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润
 出厂价
出厂价 生产成本
生产成本 检验费
检验费 调试费);
调试费);(Ⅲ)假设每台仪器是否合格相互独立,记
 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
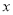 的二次函数
的二次函数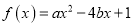 .
.(1)设集合
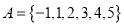 和
和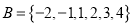 ,分别从集合
,分别从集合 中随机取一个数作为
中随机取一个数作为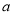 和
和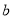 ,求函数
,求函数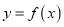 在区间
在区间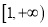 上是增函数的概率;
上是增函数的概率;(2)设点
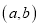 是区域
是区域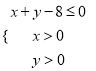 内的随机点, 求函数
内的随机点, 求函数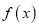 在区间
在区间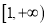 上是增函数的概率.
上是增函数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为
 ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为 ,且
,且 、
、 .若
.若 ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在某港口
 处获悉,其正东方向距离20n mile的
处获悉,其正东方向距离20n mile的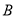 处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°距港口10n mile的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°距港口10n mile的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.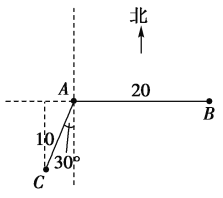
(1)求接到救援命令时救援船距渔船的距离;
(2)试问救援船在C处应朝北偏东多少度的方向沿直线前往B处救援?(已知
 )
)
相关试题

