【题目】某城市出租车的收费标准是:3千米以内(含3千米),收起步价8元;3千米以上至8千米以内(含8千米),超出3千米的部分按![]() 元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
元/千米收取;8千米以上,超出8千米的部分按2元/千米收取.
(1)计算某乘客搭乘出租车行驶7千米时应付的车费;
(2)试写出车费![]() (元)与里程
(元)与里程![]() (千米)之间的函数解析式并画出图像;
(千米)之间的函数解析式并画出图像;

(3)小陈周末外出,行程为10千米,他设计了两种方案:
方案1:分两段乘车,先乘一辆行驶5千米,下车换乘另一辆车再行5千米至目的地
方案2:只乘一辆车至目的地,试问:以上哪种方案更省钱,请说明理由.
参考答案:
【答案】(1)14元;(2)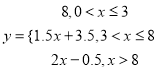 ;(3)方案二更省钱.
;(3)方案二更省钱.
【解析】试题分析:(1)根据题意,某厂乘客搭乘出租车形式7千米时应付的车费为起步价加上超出本按![]() 元/千米计算,即可求得结果;
元/千米计算,即可求得结果;
(2)利用分段函数,写出车费与里程之间的函数解析式即可;
(3)求出两种方案下的各自费用,比较即可得到结论.
试题解析:
(1) ![]() 元.
元.
(2) 

(3)方案一的费用为:22元.
方案二的费用为: ![]() 元.
元.
方案二更省钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直三棱柱
 中,底面
中,底面  是边长为2的正三角形,
是边长为2的正三角形,  是棱
是棱  的中点,且
的中点,且  .
.
(1)试在棱 上确定一点
上确定一点  ,使
,使  平面
平面  ;
;
(2)当点 在棱
在棱  中点时,求直线
中点时,求直线  与平面
与平面  所成角的大小的正弦值。
所成角的大小的正弦值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 .
.
(1)讨论函数 的极值;
的极值;
(2)当 时,
时,  ,求
,求  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
 与四棱锥
与四棱锥 的组合体中,已知
的组合体中,已知 平面
平面 ,四边形
,四边形 是平行四边形,
是平行四边形,  ,
,  ,
,  ,
,  ,设
,设 是线段
是线段 中点.
中点.
(1)求证:
 平面
平面 ;
;(2)证明:平面
 平面
平面 ;
;(3)求四棱锥
 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知α,β是平面,m,n是直线.下列命题中不正确的是 ( )
A.若m∥n,m⊥α,则n⊥α
B.若m∥α,α∩β=n,则m∥n
C.若m⊥α,m⊥β,则α∥β
D.若m⊥α, ,则α⊥β
,则α⊥β -
科目: 来源: 题型:
查看答案和解析>>【题目】图是正方体的平面展开图,在这个正方体中:①
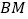 与
与  平行;②
平行;②  与
与  是异面直线;③
是异面直线;③  与
与 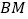 成
成  角;④
角;④  与
与  垂直;以上四个命题中,正确的是( )
垂直;以上四个命题中,正确的是( )
A.①②③
B.②④
C.②③④
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线  的参数方程为
的参数方程为  (
(  为参数).再以原点为极点,以
为参数).再以原点为极点,以  正半轴为极轴建立极坐标系,并使得它与直角坐标系
正半轴为极轴建立极坐标系,并使得它与直角坐标系  有相同的长度单位.在该极坐标系中圆
有相同的长度单位.在该极坐标系中圆  的方程为
的方程为  .
.
(1)求圆 的直角坐标方程;
的直角坐标方程;
(2)设圆 与直线
与直线  交于点
交于点  、
、  ,若点
,若点  的坐标为
的坐标为  ,求
,求  的值.
的值.
相关试题

