【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
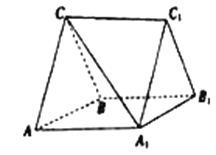
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() ;
;
(3)若![]() ,求证:平面
,求证:平面![]() 平面
平面![]() .
.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,证明四边形
,证明四边形![]() 是平行四边形,得出
是平行四边形,得出![]() ,利用线面平行的判定定理可得结论;(2)先证明
,利用线面平行的判定定理可得结论;(2)先证明![]() ,
,![]() 可得
可得![]() 平面
平面![]() ,从而
,从而![]()
![]() ; (3)根据菱形的性质以及(2)的结论可得
; (3)根据菱形的性质以及(2)的结论可得![]()
![]() ,
,![]() ,由此得
,由此得![]() 平面
平面![]() ,故而平面
,故而平面![]() 平面
平面![]() .
.
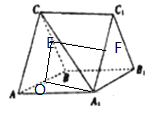
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() ,
,
∵![]() 是
是![]() 的中点,四边形
的中点,四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)连接![]() ,
,
∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]()
![]() .
.
(3)∵![]() ,
,
∴四边形![]() 是菱形,
是菱形,
∴![]() ,
,
由(2)知![]()
![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂有方木料90
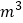 ,五合板600
,五合板600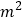 ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 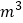 ,五合板2
,五合板2 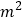 ,生产每个书橱需要方木料0.2
,生产每个书橱需要方木料0.2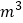 ,五合板1
,五合板1 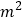 ,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1 , A1D1的中点,点P,Q分别在棱DD1 , BB1上移动,且DP=BQ=λ(0<λ<2)
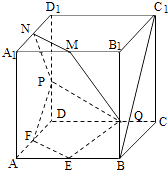
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:年入流量X
40<X<80
80≤X≤120
X>120
发电机最多可运行台数
1
2
3
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为
 ,
, ,
, ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为 ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
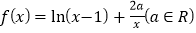 .
.(1)求
 的单调区间;
的单调区间;(2)如果当
 ,且
,且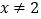 时,
时,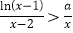 恒成立,求实数
恒成立,求实数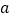 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
相关试题

