【题目】已知函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)如果当![]() ,且
,且![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的范围.
的范围.
参考答案:
【答案】(1)![]() 的单调递增区间
的单调递增区间![]() 和
和![]() ;
;![]() 的单调递减区间
的单调递减区间![]() .
.
(2)实数![]() 的取值范围是
的取值范围是![]() .
.
【解析】分析:(1)求出函数的导数,对![]() 分
分![]() 和
和![]() 两种情况讨论,即可得到函数的单调性;
两种情况讨论,即可得到函数的单调性;
(2)由题意把式子![]() 化为
化为![]() ,设
,设![]() ,
,
由(1)的结论,即可求解实数![]() 的取值范围;或把
的取值范围;或把![]() 可化为
可化为![]() ,设
,设![]() ,求得
,求得![]() 得出函数的单调性,令洛必达法则求解.
得出函数的单调性,令洛必达法则求解.
详解:(1)定义域为![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,
①当![]() 时,对称轴
时,对称轴![]() ,
,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
②当![]() 时,
时,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上是增函数,
上是增函数,
③当![]() 时,令
时,令![]() 得
得![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,
,![]() ;令
;令![]() ,解得
,解得![]() ,
,
所以![]() 的单调递增区间
的单调递增区间![]() 和
和![]() ;
;![]() 的单调递减区间
的单调递减区间![]() .
.
(2)![]() 可化为
可化为![]() ,设
,设![]() ,
,
由(1)知:
①当![]() 时,
时,![]() 在
在![]() 上是增函数,若
上是增函数,若![]() 时,
时,![]() ;
;
所以![]() ,
,
若![]() 时,
时,![]() ,所以
,所以![]() ,所以,当
,所以,当![]() 时,
时,![]() 式成立.
式成立.
②当![]() 时,
时,![]() 在
在![]() 是减函数,所以
是减函数,所以![]() 式不成立,
式不成立,
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
解法二:![]() 可化为
可化为![]() ,设
,设
![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ;
;
![]() ,
,![]() 在
在![]() 上,又
上,又![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
所以![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() 在
在![]() ,
,![]() ,
,
由洛必达法则![]()
![]() ,所以
,所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:年入流量X
40<X<80
80≤X≤120
X>120
发电机最多可运行台数
1
2
3
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,
中, ,
, ,
, ,
,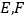 分别是
分别是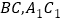 的中点.
的中点.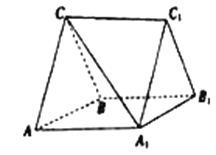
(1)证明:
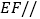 平面
平面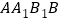 ;
;(2)证明:
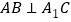 ;
;(3)若
 ,求证:平面
,求证:平面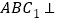 平面
平面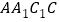 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为
 ,
, ,
, ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为 ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划在全国中学生田径比赛期间,安排6位志愿者到4个比赛场地提供服务,要求甲、乙两个比赛场地各安排一个人,剩下两个比赛场地各安排两个人,其中的小李和小王不在一起,不同的安排方案共有( )
A. 168种 B. 156种 C. 172种 D. 180种
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点M到点F(1,0)的距离比它到y轴的距离多1,记点M的轨迹为C.
(1)求轨迹C的方程;
(2)设斜率为k的直线l过定点P(﹣2,1),求直线l与轨迹C恰好有一个公共点、两个公共点、三个公共点时k的相应取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】π为圆周率,e=2.71828…为自然对数的底数.
(1)求函数f(x)= 的单调区间;
的单调区间;
(2)求e3 , 3e , eπ , πe , 3π , π3这6个数中的最大数和最小数;
(3)将e3 , 3e , eπ , πe , 3π , π3这6个数按从小到大的顺序排列,并证明你的结论.
相关试题

