【题目】计划在某水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量X(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,其中,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来4年中,至多有1年的年入流量超过120的概率;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量X限制,并有如下关系:
年入流量X | 40<X<80 | 80≤X≤120 | X>120 |
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
参考答案:
【答案】
(1)解:依题意,p1=P(40<X<80)= ![]() ,
, ![]() ,
, ![]() ,
,
由二项分布,未来4年中,至多有1年的年入流量超过120的概率为
![]() =
= ![]()
(2)解:记水电站的总利润为Y(单位,万元)
①安装1台发电机的情形,
由于水库年入流总量大于40,故一台发电机运行的概率为1,对应的年利润Y=5000,E(Y)=5000×1=5000,
②安装2台发电机的情形,
依题意,当 40<X<80时,一台发电机运行,此时Y=5000﹣800=4200,
因此P(Y=4200)=P(40<X<80)=p1= ![]() ,
,
当X≥80时,两台发电机运行,此时Y=5000×2=10000,因此,P(Y=10000)=P(X≥80)=P2+P3=0.8,
由此得Y的分布列如下
Y | 4200 | 10000 |
P | 0.2 | 0.8 |
所以E(Y)=4200×0.2+10000×0.8=8840.
③安装3台发电机的情形,
依题意,当 40<X<80时,一台发电机运行,此时Y=5000﹣1600=3400,
因此P(Y=3400)=P(40<X<80)=p1=0.2,
当80≤X≤120时,两台发电机运行,此时Y=5000×2﹣800=9200,因此,P(Y=9200)=P(80≤X≤120)=p2=0.7,
当X>120时,三台发电机运行,此时Y=5000×3=15000,因此,P(Y=15000)=P(X>120)=p3=0.1,
由此得Y的分布列如下
Y | 3400 | 9200 | 15000 |
P | 0.2 | 0.7 | 0.1 |
所以E(Y)=3400×0.2+9200×0.7+15000×0.1=8620.
综上,欲使水电站年总利润的均值达到最大,应安装发电机2台.
【解析】(1)先求出年入流量X的概率,根据二项分布,求出未来4年中,至少有1年的年入流量超过120的概率;(2)分三种情况进行讨论,分别求出一台,两台,三台的数学期望,比较即可得到
【考点精析】解答此题的关键在于理解离散型随机变量及其分布列的相关知识,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙
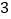 人投篮,投进的概率分别是
人投篮,投进的概率分别是 ,
,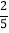 ,
, .
.(1)现
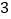 人各投篮
人各投篮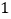 次,求
次,求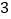 人至少一人投进的概率;
人至少一人投进的概率;(2)用
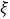 表示乙投篮
表示乙投篮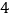 次的进球数,求随机变量
次的进球数,求随机变量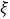 的概率分布及数学期望
的概率分布及数学期望 和方差
和方差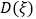 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家具厂有方木料90
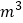 ,五合板600
,五合板600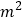 ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料0.1 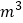 ,五合板2
,五合板2 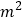 ,生产每个书橱需要方木料0.2
,生产每个书橱需要方木料0.2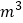 ,五合板1
,五合板1 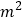 ,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大?
,出售一张书桌可获利润80元,出售一个书橱可获利润120元.请问怎样安排生产可使所得利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1 , A1D1的中点,点P,Q分别在棱DD1 , BB1上移动,且DP=BQ=λ(0<λ<2)
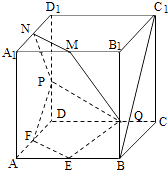
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
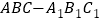 中,
中, ,
, ,
, ,
,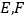 分别是
分别是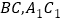 的中点.
的中点.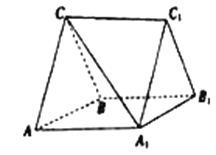
(1)证明:
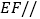 平面
平面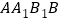 ;
;(2)证明:
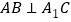 ;
;(3)若
 ,求证:平面
,求证:平面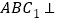 平面
平面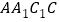 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】学校举办的集体活动中,设计了如下有奖闯关游戏:参赛选手按第一关、第二关、第三关的顺序依次闯关,若闯关成功,分别获得1分、2分、3分的奖励,游戏还规定,当选手闯过一关后,可以选择得到相应的分数,结束游戏;也可以选择继续闯下一关,若有任何一关没有闯关成功,则全部分数都归零,游戏结束。设选手甲第一关、第二关、第三关的概率分别为
 ,
, ,
, ,选手选择继续闯关的概率均为
,选手选择继续闯关的概率均为 ,且各关之间闯关成功互不影响
,且各关之间闯关成功互不影响(I)求选手甲第一关闯关成功且所得分数为零的概率
(II)设该学生所得总分数为X,求X的分布列与数学期望
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
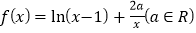 .
.(1)求
 的单调区间;
的单调区间;(2)如果当
 ,且
,且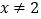 时,
时,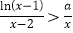 恒成立,求实数
恒成立,求实数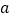 的范围.
的范围.
相关试题

