【题目】先阅读下列不等式的证法,再解决后面的问题:
已知![]() ,
,![]() ,求证:
,求证:![]() .
.
证明:构造函数![]() ,
,
即![]()
![]() .
.
因为对一切![]() ,恒有
,恒有![]() ,
,
所以![]() ,从而得
,从而得![]() .
.
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你推广的结论加以证明.
参考答案:
【答案】(1)若![]() ,
,![]() ,…
,…![]() ,
,![]() ,则
,则![]() ;(2)略.
;(2)略.
【解析】
试题(1)根据题干中的式子,类比写出求证: ![]() ;(2)构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2,展开后是关于x的二次函数,函数大于等于0恒成立,即判别式小于等于0,从而得证.
;(2)构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2,展开后是关于x的二次函数,函数大于等于0恒成立,即判别式小于等于0,从而得证.
解析:
(1)解:若a1,a2,…,an∈R,a1+a2+…+an=1.
求证: ![]() .
.
(2)证明:构造函数f(x)=(x-a1)2+(x-a2)2+…+(x-an)2=nx2-2(a1+a2+…+an)x+![]() =nx2-2x+
=nx2-2x+![]() ,
,
因为对一切x∈R,都有f(x)≥0,
所以Δ=4-4n(![]() )≤0,
)≤0,
从而证得![]() ≥.
≥.![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若
 是
是 的极大值点,求
的极大值点,求 的值;
的值;(2)若
 在
在 上只有一个零点,求
上只有一个零点,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有两台不同机器A和B生产同一种产品各10万件,现从各自生产的产品中分别随机抽取二十件,进行品质鉴定,鉴定成绩的茎叶图如下所示:

该产品的质量评价标准规定:鉴定成绩达到
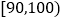 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到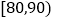 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到 的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.(1)从等级为优秀的样本中随机抽取两件,记
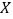 为来自B机器生产的产品数量,写出
为来自B机器生产的产品数量,写出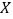 的分布列,并求
的分布列,并求 的数学期望;
的数学期望;(2)完成下列
 列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过0.05的情况下,认为B机器生产的产品比A机器生产的产品好;
列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过0.05的情况下,认为B机器生产的产品比A机器生产的产品好;A生产的产品
B生产的产品
合计
良好以上(含良好)
合格
合计
(3)已知优秀等级产品的利润为12元/件,良好等级产品的利润为10元/件,合格等级产品的利润为5元/件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗?
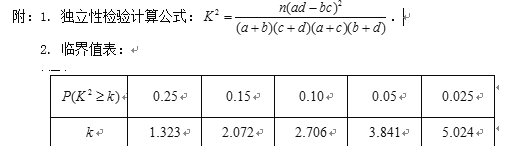
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,函数
,函数 .
.(1)若
 无零点,求实数
无零点,求实数 的取值范围;
的取值范围;(2)若
 有两个相异零点
有两个相异零点 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知椭圆
中,已知椭圆 经过点
经过点 ,离心率为
,离心率为 .
.(1)求
 的方程;
的方程;(2)过
 的左焦点
的左焦点 且斜率不为
且斜率不为 的直线
的直线 与
与 相交于
相交于 ,
, 两点,线段
两点,线段 的中点为
的中点为 ,直线
,直线 与直线
与直线 相交于点
相交于点 ,若
,若 为等腰直角三角形,求
为等腰直角三角形,求 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个2×2的列联表;
(2)试判断能否有99.5%的把握认为“考试成绩与班级有关”?参考公式:

 ;n=a+b+c+d
;n=a+b+c+dP(
 >k)
>k)0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

