【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]()
![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 存在极值点
存在极值点![]() ,且
,且![]() ,其中
,其中![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,函数
,函数![]() ,求证:
,求证:![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() .
.
参考答案:
【答案】(1)当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)求出![]() 的导数,讨论
的导数,讨论![]() 时,
时,![]() ,
,![]() 在
在![]() 上递增;当
上递增;当![]() 时,由导数大
时,由导数大
于![]() ,可得增区间;导数小于
,可得增区间;导数小于![]() ,可得减区间;(2)
,可得减区间;(2)![]() ,可得
,可得![]() ,分别计算
,分别计算![]() ,
,![]() ,化简整理即可得证;(3)要证
,化简整理即可得证;(3)要证![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() ,即证在
,即证在![]() 上存在
上存在![]() ,
,![]() ,使得
,使得![]() ,运用单调性和极值,化简整理即可得证.
,运用单调性和极值,化简整理即可得证.
试题解析:(1)解:由![]() ,可得
,可得![]() .
.
下面分两种情况讨论:
①当![]() 时,有
时,有![]() 恒成立,所以
恒成立,所以![]() 的单调递增区间为
的单调递增区间为![]() ;
;
②当![]() 时,令
时,令![]() ,解得
,解得![]() ,或
,或![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| 极大值 |
| 极小值 |
|
所以![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ,
,![]() .
.
(2)证明:因为![]() 存在极值点,所以由(1)知
存在极值点,所以由(1)知![]() ,且
,且![]() ,
,
由题意,得![]() ,即
,即![]() ,
,
进而![]() ,
,
又![]()
![]()
![]() ,
,
即为![]() ,即有
,即有![]() ,即为
,即为![]() .
.
(3)要证![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() ,即证在
,即证在![]() 上存在
上存在![]() ,
,![]() ,使得
,使得![]() ,
,
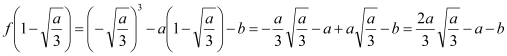 ,
,
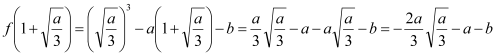 ,
,
![]() ,
,![]() ,
,![]() ,
,
由于![]() ,
,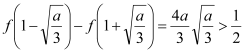 成立.
成立.
综上可得,![]() 在区间
在区间![]() 上的最大值不小于
上的最大值不小于![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表
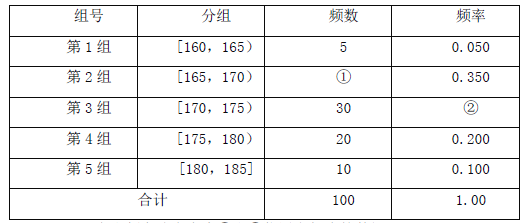
(Ⅰ)求出频率分布表中①和②位置上相应的数据;
(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5 组中用分层抽样的方法抽取6 名学生进行体能测试,求第3,4,5 组每组各应抽取多少名学生进行测试;
(Ⅲ)在(Ⅱ)的前提下,学校决定在6 名学生中随机抽取2 名学生进行引体向上测试,求第4 组中至少有一名学生被抽中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂每日生产某种产品
 吨,当日生产的产品当日销售完毕,产品价格随产品产量而变化,当
吨,当日生产的产品当日销售完毕,产品价格随产品产量而变化,当 时,每日的销售额
时,每日的销售额 (单位:万元)与当日的产量
(单位:万元)与当日的产量 满足
满足 ,当日产量超过
,当日产量超过 吨时,销售额只能保持日产量
吨时,销售额只能保持日产量 吨时的状况.已知日产量为
吨时的状况.已知日产量为 吨时销售额为
吨时销售额为 万元,日产量为
万元,日产量为 吨时销售额为
吨时销售额为 万元.
万元.(1)把每日销售额
 表示为日产量
表示为日产量 的函数;
的函数;(2)若每日的生产成本
 (单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.(注:计算时取
(单位:万元),当日产量为多少吨时,每日的利润可以达到最大?并求出最大值.(注:计算时取 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学家里订了一份报纸,送报人每天都在早上6 : 207 : 40之间将报纸送达,该同学需要早上7 : 008 : 00之间出发上学,则这位同学在离开家之前能拿到报纸的概率为 ( )
A.
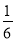 B.
B. 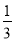 C.
C. 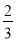 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 ,则下面结论正确的是 ( )
,则下面结论正确的是 ( )A. 把
 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的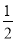 倍, 纵坐标不变,再把得到的曲线向左平移
倍, 纵坐标不变,再把得到的曲线向左平移 个单位长度, 得到曲线
个单位长度, 得到曲线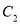
B. 把
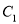 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的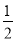 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移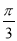 个单位长度,得到曲线
个单位长度,得到曲线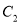
C. 把
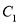 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的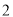 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移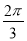 个单位长度,得到曲线
个单位长度,得到曲线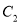
D. 把
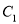 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的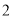 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移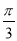 个单位长度,得到曲线
个单位长度,得到曲线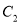
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正确命题有__________.
①“
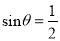 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件②如果命题“
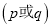 ”为假命题,则
”为假命题,则 中至多有一个为真命题
中至多有一个为真命题③设
 ,若
,若 ,则
,则 的最小值为
的最小值为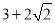
④函数
 在
在 上存在
上存在 ,使
,使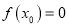 ,则a的取值范围
,则a的取值范围 或
或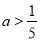 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
 中,椭圆
中,椭圆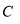 :
: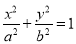 (
(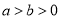 )的离心率是
)的离心率是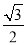 ,抛物线
,抛物线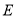 :
: 的焦点
的焦点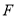 是
是 的一个顶点.
的一个顶点.(1)求椭圆
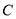 的方程;
的方程;(2)设
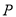 是
是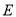 上的动点,且位于第一象限,
上的动点,且位于第一象限,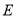 在点
在点 处的切线
处的切线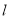 与
与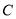 交于不同的两点
交于不同的两点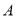 ,
,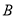 ,线段
,线段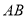 的中点为
的中点为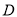 ,直线
,直线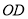 与过
与过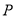 且垂直于
且垂直于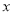 轴的直线交于点
轴的直线交于点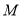 .
.(i)求证:点
 在定直线上;
在定直线上;(ii)直线
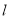 与
与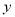 轴交于点
轴交于点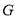 ,记△
,记△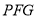 的面积为
的面积为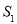 ,△
,△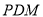 的面积为
的面积为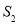 ,求
,求 的最大值及取得最大值时点
的最大值及取得最大值时点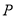 的坐标.
的坐标.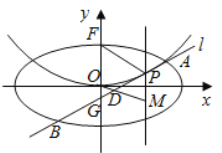
相关试题

