【题目】平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() (
(![]() )的离心率是
)的离心率是![]() ,抛物线
,抛物线![]() :
:![]() 的焦点
的焦点![]() 是
是![]() 的一个顶点.
的一个顶点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上的动点,且位于第一象限,
上的动点,且位于第一象限,![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与过
与过![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() .
.
(i)求证:点![]() 在定直线上;
在定直线上;
(ii)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,记△
,记△![]() 的面积为
的面积为![]() ,△
,△![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值及取得最大值时点
的最大值及取得最大值时点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)![]() ;(2)(i)证明见解析,(ii)
;(2)(i)证明见解析,(ii)![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() .
.
【解析】
试题分析:(1)运用椭圆的离心率公式和抛物线的焦点坐标,以及椭圆的![]() ,
,![]() ,
,![]() 的关系,解得
的关系,解得![]() ,
,![]() ,
,
进而得到椭圆的方程;(2)(i)设![]() ,运用导数求得切线的斜率和方程,代入椭圆方程,运用韦达定理,可得中点
,运用导数求得切线的斜率和方程,代入椭圆方程,运用韦达定理,可得中点![]() 的坐标,求得
的坐标,求得![]() 的方程,再令
的方程,再令![]() ,可得
,可得![]() .进而得到定直线;(ii)由直线
.进而得到定直线;(ii)由直线![]() 的方程为
的方程为![]() ,令
,令![]() ,可得
,可得![]() ,运用三角形的面积公式,可得
,运用三角形的面积公式,可得![]() ,
,![]() ,化简整理,再
,化简整理,再![]() ,整理可得
,整理可得![]() 的二次方程,进而得到最大值及此时
的二次方程,进而得到最大值及此时![]() 的坐标.
的坐标.
试题解析:(1)由题意知![]() ,可得
,可得![]() ,
,
因为抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,
,![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)(i)设![]() (
(![]() ),由
),由![]() 可得
可得![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() ,
,
因此直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,![]() ,联立方程
,联立方程
得![]() ,
,
由![]() ,得
,得![]() 且
且![]() ,
,
因此![]() ,
,
将其代入![]() ,得
,得![]() ,
,
因为![]() ,所以直线
,所以直线![]() 方程为
方程为![]() ,
,
联立方程 得点
得点![]() 的纵坐标为
的纵坐标为![]() ,
,
即点![]() 在定直线
在定直线![]() 上.
上.
(ii)由(i)知直线![]() 方程为
方程为![]() ,令
,令![]() ,得
,得![]() ,∴
,∴![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,所以
,所以![]() ,
,
令![]() ,则
,则![]() ,则
,则![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 取得最大值
取得最大值![]() ,此时
,此时![]() ,满足
,满足![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,因此
,因此![]() 的最大值为
的最大值为![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
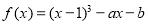 ,
,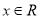 ,其中
,其中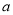 ,
,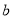
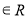 .
.(1)求
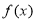 的单调区间;
的单调区间;(2)若
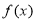 存在极值点
存在极值点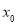 ,且
,且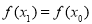 ,其中
,其中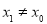 ,求证:
,求证: ;
;(3)设
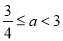 ,函数
,函数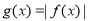 ,求证:
,求证: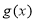 在区间
在区间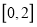 上的最大值不小于
上的最大值不小于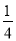 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线
 ,则下面结论正确的是 ( )
,则下面结论正确的是 ( )A. 把
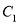 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的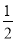 倍, 纵坐标不变,再把得到的曲线向左平移
倍, 纵坐标不变,再把得到的曲线向左平移 个单位长度, 得到曲线
个单位长度, 得到曲线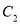
B. 把
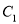 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的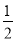 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移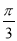 个单位长度,得到曲线
个单位长度,得到曲线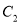
C. 把
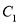 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的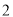 倍 ,纵坐标不变,再把得到的曲线向左平移
倍 ,纵坐标不变,再把得到的曲线向左平移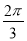 个单位长度,得到曲线
个单位长度,得到曲线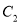
D. 把
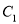 上各点的横坐标伸长到原来的
上各点的横坐标伸长到原来的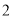 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移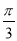 个单位长度,得到曲线
个单位长度,得到曲线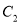
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列正确命题有__________.
①“
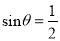 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件②如果命题“
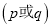 ”为假命题,则
”为假命题,则 中至多有一个为真命题
中至多有一个为真命题③设
 ,若
,若 ,则
,则 的最小值为
的最小值为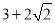
④函数
 在
在 上存在
上存在 ,使
,使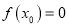 ,则a的取值范围
,则a的取值范围 或
或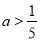 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
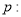 方程
方程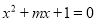 有两个不等的负根,
有两个不等的负根, 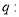 方程
方程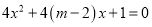 无实根,若“
无实根,若“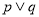 ”为真,“
”为真,“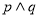 ”为假,求实数
”为假,求实数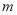 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
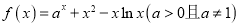 .
.(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)求函数
 的单调区间;
的单调区间;(3)若存在
 ,使得
,使得 (
( 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)(本小题满分12分)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
组号
分组
频数
频率
第一组
[230,235)
8
0.16
第二组
[235,240)
①
0.24
第三组
[240,245)
15
②
第四组
[245,250)
10
0.20
第五组
[250,255]
5
0.10
合 计
50
1.00
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
相关试题

