【题目】下列结论中正确的个数有( )
(1)数列{an},{bn}都是等差数列,则数列{an+bn}也一定是等差数列;
(2)数列{an},{bn}都是等比数列,则数列{an+bn}也一定是等比数列;
(3)等差数列{an}的首项为a1 , 公差为d,取出数列中的所有奇数项,组成一个新的数列,一定还是等差数列;
(4) G为a,b的等比中项G2=ab.
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:在(1)中,数列{an},{bn}都是等差数列,
当这两个等差数列的项数不相同时,数列{an+bn}不一定是等差数列,故(1)错误;
在(2)中,数列{an},{bn}都是等比数列,
当这两个等比数列的项数不相同时,数列{an+bn}不一定是等比数列,故(2)错误;
在(3)中,等差数列{an}的所有奇数项构成一个首项为a1 , 公差为2d的等差数列,故(3)正确;
在(4)中,由等比中项的定义得G为a,b的等比中项G2=ab.故(4)正确.
故选:B.
【考点精析】解答此题的关键在于理解等差数列的通项公式(及其变式)的相关知识,掌握通项公式:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上
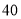 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为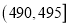 ,
,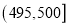 , ,
, ,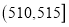 ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.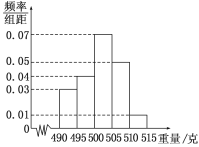
(1)根据频率分布直方图,求重量超过
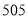 克的产品数量;
克的产品数量;(2)在上述抽取的
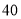 件产品中任取
件产品中任取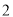 件,设
件,设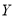 为重量超过
为重量超过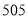 克的产品数量,求
克的产品数量,求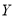 的分布列;
的分布列;(3)从该流水线上任取
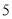 件产品,求恰有
件产品,求恰有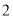 件产品的重量超过
件产品的重量超过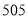 克的概率.
克的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】记等比数列{an}前n项和为Sn , 已知a1+a3=30,3S1 , 2S2 , S3成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=3,bn+1﹣3bn=3an , 求数列{bn}的前n项和Bn;
(3)删除数列{an}中的第3项,第6项,第9项,…,第3n项,余下的项按原来的顺序组成一个新数列,记为{cn},{cn}的前n项和为Tn , 若对任意n∈N* , 都有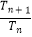 >a,试求实数a的最大值.
>a,试求实数a的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:
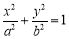 (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为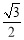 .
.(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=﹣f(x),当﹣1≤x<1时,f(x)=x3 , 若函数g(x)=f(x)﹣loga|x|至少6个零点,则a取值范围是( )
A.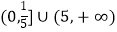
B.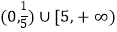
C.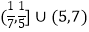
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分16分)
设函数
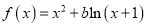 .
.(1)若
 =1时,函数
=1时,函数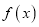 取最小值,求实数
取最小值,求实数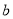 的值;
的值;(2)若函数
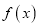 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数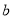 的取值范围;
的取值范围;(3)若
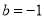 ,证明对任意正整数
,证明对任意正整数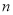 ,不等式
,不等式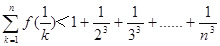 都成立.
都成立.
相关试题

