【题目】(本题满分16分)
设函数![]() .
.
(1)若![]() =1时,函数
=1时,函数![]() 取最小值,求实数
取最小值,求实数![]() 的值;
的值;
(2)若函数![]() 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意正整数
,证明对任意正整数![]() ,不等式
,不等式![]() 都成立.
都成立.
参考答案:
【答案】(1)- 4.(2)![]() (3)详见解析
(3)详见解析
【解析】试题分析:(1)利用导数求开区间函数最值,先从导函数出发,探求极值点即为最值点,最后需列表验证:由![]() 得
得![]() (2)函数
(2)函数![]() 在定义域上是单调函数,即导函数不变号,
在定义域上是单调函数,即导函数不变号, ![]() ≥0或
≥0或![]() ≤0在( - 1,+ ∞)上恒成立. 即2x2+2x+b≥0在( - 1,+ ∞)上恒成立或2x2+2x+b≤0在( - 1,+ ∞)上恒成立,利用变量分离及函数最值可得:实数b的取值范围是
≤0在( - 1,+ ∞)上恒成立. 即2x2+2x+b≥0在( - 1,+ ∞)上恒成立或2x2+2x+b≤0在( - 1,+ ∞)上恒成立,利用变量分离及函数最值可得:实数b的取值范围是![]() .(3)证明和项不等式,关键分析出和项与通项关系:
.(3)证明和项不等式,关键分析出和项与通项关系: ![]() 即证当
即证当![]() 时,有f(x) <x3.这可利用导数给予证明
时,有f(x) <x3.这可利用导数给予证明
试题解析:(1)由x + 1>0得x> – 1∴f(x)的定义域为( - 1,+ ∞),
对x∈ ( - 1,+ ∞),都有f(x)≥f(1),∴f(1)是函数f(x)的最小值,故有f/(1) = 0,
![]() 解得b=" -" 4. 经检验,列表(略),合题意;
解得b=" -" 4. 经检验,列表(略),合题意;
(2)∵![]() 又函数
又函数![]() 在定义域上是单调函数,
在定义域上是单调函数,
∴![]() ≥0或
≥0或![]() ≤0在( - 1,+ ∞)上恒成立.
≤0在( - 1,+ ∞)上恒成立.
若![]() ≥0,∵x + 1>0,∴2x2+2x+b≥0在( - 1,+ ∞)上恒成立,
≥0,∵x + 1>0,∴2x2+2x+b≥0在( - 1,+ ∞)上恒成立,
即b≥-2x2-2x =![]() 恒成立,由此得b≥
恒成立,由此得b≥![]() ;
;
若![]() ≤0, ∵x + 1>0, ∴2x2+2x+b≤0,即b≤- (2x2+2x)恒成立,
≤0, ∵x + 1>0, ∴2x2+2x+b≤0,即b≤- (2x2+2x)恒成立,
因-(2x2+2x) 在( - 1,+ ∞)上没有最小值,∴不存在实数b使f(x) ≤0恒成立.
综上所述,实数b的取值范围是![]() .
.
(3)当b=" -" 1时,函数f(x) = x2- ln(x+1),令函数h(x)="f(x)" – x3= x2– ln(x+1) – x3,
则h/(x) =" -" 3x2+2x -![]() ,
,
∴当![]() 时,h/(x)<0所以函数h(x)在
时,h/(x)<0所以函数h(x)在![]() 上是单调递减.
上是单调递减.
又h(0)=0,∴当![]() 时,恒有h(x) <h(0)=0,即x2– ln(x+1) <x3恒成立.
时,恒有h(x) <h(0)=0,即x2– ln(x+1) <x3恒成立.
故当![]() 时,有f(x) <x3..
时,有f(x) <x3..
∵![]() 取
取![]() 则有
则有![]()
∴![]() ,故结论成立。
,故结论成立。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的个数有( )
(1)数列{an},{bn}都是等差数列,则数列{an+bn}也一定是等差数列;
(2)数列{an},{bn}都是等比数列,则数列{an+bn}也一定是等比数列;
(3)等差数列{an}的首项为a1 , 公差为d,取出数列中的所有奇数项,组成一个新的数列,一定还是等差数列;
(4) G为a,b的等比中项G2=ab.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分16分)
在平面直角坐标系xOy中,椭圆C:
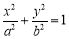 (a>b>0)的上顶点到焦点的距离为2,离心率为
(a>b>0)的上顶点到焦点的距离为2,离心率为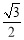 .
.(1)求a,b的值.
(2)设P是椭圆C长轴上的一个动点,过点P作斜率为k的直线l交椭圆C于A、B两点.
(ⅰ)若k=1,求△OAB面积的最大值;
(ⅱ)若PA2+PB2的值与点P的位置无关,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数y=f(x)对任意的x都满足f(x+1)=﹣f(x),当﹣1≤x<1时,f(x)=x3 , 若函数g(x)=f(x)﹣loga|x|至少6个零点,则a取值范围是( )
A.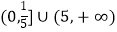
B.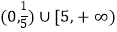
C.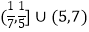
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
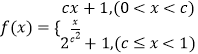 ,且
,且 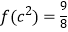 .
.
(1)求实数c的值;
(2)解不等式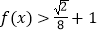 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的顶点在原点,焦点在x轴上,且抛物线上有一点P(4,m)到焦点的距离为6.
(Ⅰ)求抛物线C的方程;
(Ⅱ)若抛物线C与直线y=kx﹣2相交于不同的两点A、B,且AB中点横坐标为2,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
在正三棱柱
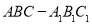 中,点
中,点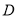 是
是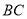 的中点,
的中点, .
.(1)求证:
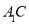 ∥平面
∥平面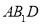 ;
;(2)试在棱
 上找一点
上找一点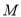 ,使
,使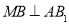 .
.
相关试题

