【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
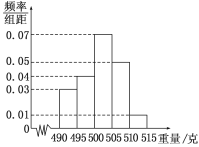
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
参考答案:
【答案】(1)![]() (件);
(件);
(2)Y的分布列为
| 0 | 1 | 2 |
P |
|
|
|
(3)![]() .
.
【解析】
试题分析:(1)根据频率分布直方图即可求出;(2)求![]() 的分布列;由于
的分布列;由于![]() 为重量超过
为重量超过![]() 克的产品数量,抽取的
克的产品数量,抽取的![]() 件产品中任取
件产品中任取![]() 件,因此
件,因此![]() 的可能取值为0,1,2.由古典概型的概率求法,分别求出概率,即得分布列;(3)从该流水线上任取
的可能取值为0,1,2.由古典概型的概率求法,分别求出概率,即得分布列;(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率,这符合二项分布,利用二项分布即可求出恰有
克的概率,这符合二项分布,利用二项分布即可求出恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
试题解析:(1)根据频率分布直方图可知,重量超过505克的产品数量为
![]() (件). (/span>2分)
(件). (/span>2分)
(2)![]() 的可能取值为0,1,2. (3分)
的可能取值为0,1,2. (3分)
![]() (4分)
(4分)
![]() (5分)
(5分)
![]() (6分)
(6分)
Y的分布列为
| 0 | 1 | 2 |
P |
|
|
|
(3)利用样本估计总体,该流水线上产品重量超过505克的概率为0.3 (8分)
令![]() 为任取的5件产品中重量超过505克的产品数量,
为任取的5件产品中重量超过505克的产品数量,
则![]() , (10分)
, (10分)
故所求概率为![]() (12分)
(12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分14分)如图,已知椭圆
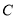 :
: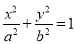 ,其左右焦点为
,其左右焦点为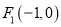 及
及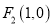 ,过点
,过点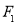 的直线交椭圆
的直线交椭圆 于
于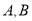 两点,线段
两点,线段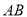 的中点为
的中点为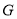 ,
,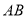 的中垂线与
的中垂线与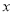 轴和
轴和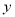 轴分别交于
轴分别交于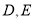 两点,且
两点,且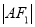 、
、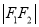 、
、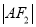 构成等差数列.
构成等差数列.
(1)求椭圆
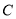 的方程;
的方程;(2)记△
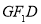 的面积为
的面积为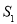 ,△
,△ (
(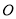 为原点)的面积为
为原点)的面积为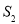 .试问:是否存在直线
.试问:是否存在直线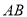 ,使得
,使得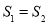 ?说明理由.
?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220.240),[240,260),[260,280),[280,300)分组的频率分布直方图如图.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为,[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户? -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)设数列
分)设数列 的前
的前 项和为
项和为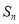 ,已知
,已知 ,
, ,
, .
.(1)求数列
 的通项公式;
的通项公式;(2)证明:对一切正整数
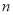 ,有
,有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】记等比数列{an}前n项和为Sn , 已知a1+a3=30,3S1 , 2S2 , S3成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=3,bn+1﹣3bn=3an , 求数列{bn}的前n项和Bn;
(3)删除数列{an}中的第3项,第6项,第9项,…,第3n项,余下的项按原来的顺序组成一个新数列,记为{cn},{cn}的前n项和为Tn , 若对任意n∈N* , 都有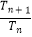 >a,试求实数a的最大值.
>a,试求实数a的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论中正确的个数有( )
(1)数列{an},{bn}都是等差数列,则数列{an+bn}也一定是等差数列;
(2)数列{an},{bn}都是等比数列,则数列{an+bn}也一定是等比数列;
(3)等差数列{an}的首项为a1 , 公差为d,取出数列中的所有奇数项,组成一个新的数列,一定还是等差数列;
(4) G为a,b的等比中项G2=ab.
A.1个
B.2个
C.3个
D.4个
相关试题

