【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的单调区间.
的单调区间.
(2)试问:是否存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
参考答案:
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() (2)存在实数
(2)存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立
恒成立
【解析】
(1)当![]() 时,得
时,得![]() ,求得
,求得![]() ,进而求解函数的单调区间;
,进而求解函数的单调区间;
(2)假设存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立,利用导数求得函数的单调性和最值,分类讨论,即可求解。
恒成立,利用导数求得函数的单调性和最值,分类讨论,即可求解。
(1)当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
故![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)![]() ,
,![]() .
.
假设存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立.
恒成立.
当![]() 时,
时,![]() 对
对![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,又
,又![]() ,则
,则![]() .
.
当![]() 时,
时,![]() 对
对![]() 恒成立,则
恒成立,则![]() 在
在![]() 上单调递增,
上单调递增,
从而![]() ,又
,又![]() ,所以
,所以![]() .
.
当![]() 时,令
时,令![]() ,得
,得![]() ,
,
若![]() ,
,![]() ;若
;若![]() ,
,![]() .
.
从而![]() ,则
,则![]() .
.
令![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递增,
上单调递增,
则![]() ,从而
,从而![]() 不可能成立.
不可能成立.
综上,存在实数![]() ,使得
,使得![]() 对
对![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为
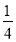 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为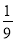 ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利
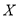 元,求
元,求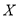 的分布列,并求出均值
的分布列,并求出均值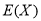 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某脐橙种植基地记录了10棵脐橙树在未使用新技术的年产量(单位:
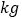 )和使用了新技术后的年产量的数据变化,得到表格如下:
)和使用了新技术后的年产量的数据变化,得到表格如下:未使用新技术的10棵脐橙树的年产量
第一棵
第二棵
第三棵
第四棵
第五棵
第六棵
第七棵
第八棵
第九棵
第十棵
年产量
30
32
30
40
40
35
36
45
42
30
使用了新技术后的10棵脐橙树的年产量
第一棵
第二棵
第三棵
第四棵
第五棵
第六棵
第七棵
第八棵
第九棵
第十棵
年产量
40
40
35
50
55
45
42
50
51
42
已知该基地共有20亩地,每亩地有50棵脐橙树.
(1)估计该基地使用了新技术后,平均1棵脐橙树的产量;
(2)估计该基地使用了新技术后,脐橙年总产量比未使用新技术将增产多少?
(3)由于受市场影响,导致使用新技术后脐橙的售价由原来(未使用新技术时)的每千克10元降为每千克9元,试估计该基地使用新技术后脐橙年总收入比原来增加的百分数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
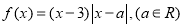 .
.(1)若
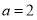 ,求函数f(x)的单调递增区间;
,求函数f(x)的单调递增区间;(2)若
 ,求函数
,求函数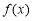 在区间
在区间 上的值域.
上的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
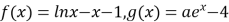 (
(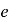 为自然对数的底数,
为自然对数的底数,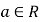 ).
).(1)求函数
 在点
在点 处的切线方程;
处的切线方程;(2)若对于任意
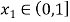 ,存在
,存在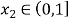 ,使得
,使得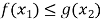 ,求
,求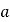 的取值范围;
的取值范围;(3)若
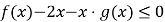 恒成立,求
恒成立,求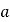 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点
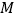 在正视图上的对应点为
在正视图上的对应点为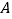 ,圆柱表面上的点
,圆柱表面上的点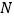 在左视图上的对应点为
在左视图上的对应点为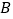 ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从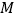 到
到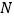 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )
A.
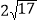 B.
B. 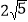 C.
C. 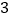 D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】设
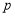 :实数
:实数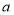 满足不等式
满足不等式 ,
,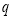 :函数
:函数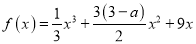 无极值点.
无极值点.(1)若“
 ”为假命题,“
”为假命题,“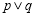 ”为真命题,求实数
”为真命题,求实数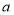 的取值范围;
的取值范围;(2)若“
 为真命题”是“
为真命题”是“ ”的必要不充分条件,求正整数
”的必要不充分条件,求正整数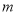 的值.
的值.
相关试题

