【题目】已知奇函数f(x)满足f(x+2)=f(x﹣2),当x∈(0,1)时,f(x)=3x , 则f( ![]() )= .
)= .
参考答案:
【答案】![]()
【解析】解:由题意可得f(x+4)=f[(x+2)﹣2]=f(x),
故函数f(x)的周期T=4,又函数为奇函数,故有f(﹣x)=﹣f(x),
∵当x∈(0,1)时,f(x)=3x ,
∴f(0.5)= ![]() ,
,
∴f( ![]() )=﹣f(0.5)=
)=﹣f(0.5)= ![]() .
.
所以答案是: ![]() .
.
【考点精析】本题主要考查了函数奇偶性的性质和函数的值的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
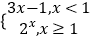 ,则满足f(f(a))=2f(a)的a的取值范围是( )
,则满足f(f(a))=2f(a)的a的取值范围是( )
A.[ ,1]
,1]
B.[0,1]
C.[ ,+∞)
,+∞)
D.[1,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
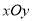 中,
中, 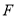 是抛物线
是抛物线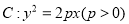 的焦点,
的焦点, 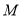 是抛物线
是抛物线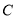 上的任意一点,当
上的任意一点,当 位于第一象限内时,
位于第一象限内时, 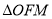 外接圆的圆心到抛物线
外接圆的圆心到抛物线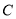 准线的距离为
准线的距离为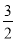 .
.(1)求抛物线
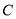 的方程;
的方程;(2)过
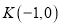 的直线
的直线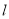 交抛物线
交抛物线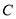 于
于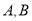 两点,且
两点,且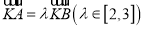 ,点
,点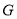 为
为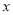 轴上一点,且
轴上一点,且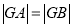 ,求点
,求点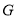 的横坐标
的横坐标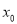 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条巡逻船由南向北行驶,在
 处测得山顶
处测得山顶 在北偏东
在北偏东 方向上,匀速向北航行
方向上,匀速向北航行 分钟到达
分钟到达 处,测得山顶
处,测得山顶 位于北偏东
位于北偏东 方向上,此时测得山顶
方向上,此时测得山顶 的仰角
的仰角 ,若山高为
,若山高为 千米,
千米,(1)船的航行速度是每小时多少千米?
(2)若该船继续航行
 分钟到达
分钟到达 处,问此时山顶位于
处,问此时山顶位于 处的南偏东什么方向?
处的南偏东什么方向?
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列不等式:
1+ ,1+
,1+ 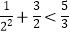 ,
,
1+ +
+  +
+ 

…
照此规律,第五个不等式为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
已知曲线
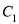 的极坐标方程为
的极坐标方程为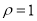 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为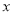 的正半轴,建立平面直角坐标系
的正半轴,建立平面直角坐标系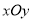 .
.(1)若曲线
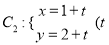 为参数)与曲线
为参数)与曲线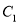 相交于两点
相交于两点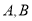 ,求
,求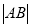 ;
;(2)若
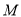 是曲线
是曲线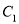 上的动点,且点
上的动点,且点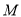 的直角坐标为
的直角坐标为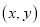 ,求
,求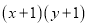 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t
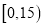
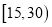
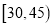
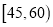
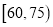
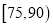
男同学人数
7
11
15
12
2
1
女同学人数
8
9
17
13
3
2
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为
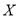 ,求
,求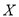 的分布列和数学期望
的分布列和数学期望
相关试题

