【题目】设函数f(x)= ![]() ,则满足f(f(a))=2f(a)的a的取值范围是( )
,则满足f(f(a))=2f(a)的a的取值范围是( )
A.[ ![]() ,1]
,1]
B.[0,1]
C.[ ![]() ,+∞)
,+∞)
D.[1,+∞)
参考答案:
【答案】C
【解析】解:令f(a)=t,
则f(t)=2t ,
当t<1时,3t﹣1=2t ,
由g(t)=3t﹣1﹣2t的导数为g′(t)=3﹣2tln2,
在t<1时,g′(t)>0,g(t)在(﹣∞,1)递增,
即有g(t)<g(1)=0,
则方程3t﹣1=2t无解;
当t≥1时,2t=2t成立,
由f(a)≥1,即3a﹣1≥1,解得a≥ ![]() ,且a<1;
,且a<1;
或a≥1,2a≥1解得a≥0,即为a≥1.
综上可得a的范围是a≥ ![]() .
.
故选C.
令f(a)=t,则f(t)=2t , 讨论t<1,运用导数判断单调性,进而得到方程无解,讨论t≥1时,以及a<1,a≥1,由分段函数的解析式,解不等式即可得到所求范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数f(x),当x>0时f(x)=x+
 ,则f(﹣1)=( )
,则f(﹣1)=( )
A.1
B.2
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两家快递公司其“快递小哥”的日工资方案如下:甲公司规定底薪
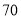 元,每单抽成
元,每单抽成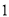 元;乙公司规定底薪
元;乙公司规定底薪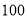 元,每日前
元,每日前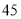 单无抽成,超过
单无抽成,超过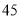 单的部分每单抽成
单的部分每单抽成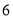 元
元(1)设甲乙快递公司的“快递小哥”一日工资
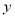 (单位:元)与送货单数
(单位:元)与送货单数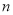 的函数关系式为
的函数关系式为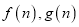 ,求
,求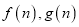 ;
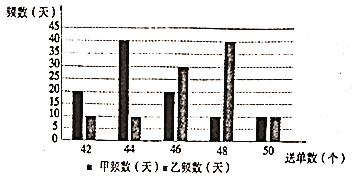
;(2)假设同一公司的“快递小哥”一日送货单数相同,现从两家公司各随机抽取一名“快递小哥”,并记录其
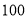 天的送货单数,得到如下条形图:
天的送货单数,得到如下条形图:若将频率视为概率,回答下列问题:
①记乙快递公司的“快递小哥”日工资为
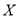 (单位:元),求
(单位:元),求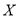 的分布列和数学期望;
的分布列和数学期望;②小赵拟到两家公司中的一家应聘“快递小哥”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的命题有__________.
①回归直线
 恒过样本点的中心
恒过样本点的中心 ,且至少过一个样本点;
,且至少过一个样本点;②将一组数据的每个数据都加一个相同的常数后,方差不变;
③用相关指数
 来刻画回归效果,
来刻画回归效果,  越接近
越接近 ,说明模型的拟合效果越好;
,说明模型的拟合效果越好;④用系统抽样法从
 名学生中抽取容量为
名学生中抽取容量为 的样本,将
的样本,将 名学生从
名学生从 编号,按编号顺序平均分成
编号,按编号顺序平均分成 组(
组( 号,
号,  号,
号,  号),若第
号),若第 组抽出的号码为
组抽出的号码为 ,则第一组中用抽签法确定的号码为
,则第一组中用抽签法确定的号码为 号.
号. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
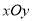 中,
中, 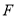 是抛物线
是抛物线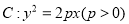 的焦点,
的焦点, 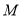 是抛物线
是抛物线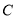 上的任意一点,当
上的任意一点,当 位于第一象限内时,
位于第一象限内时, 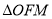 外接圆的圆心到抛物线
外接圆的圆心到抛物线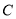 准线的距离为
准线的距离为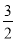 .
.(1)求抛物线
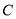 的方程;
的方程;(2)过
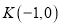 的直线
的直线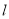 交抛物线
交抛物线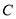 于
于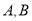 两点,且
两点,且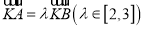 ,点
,点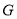 为
为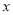 轴上一点,且
轴上一点,且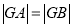 ,求点
,求点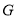 的横坐标
的横坐标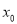 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条巡逻船由南向北行驶,在
 处测得山顶
处测得山顶 在北偏东
在北偏东 方向上,匀速向北航行
方向上,匀速向北航行 分钟到达
分钟到达 处,测得山顶
处,测得山顶 位于北偏东
位于北偏东 方向上,此时测得山顶
方向上,此时测得山顶 的仰角
的仰角 ,若山高为
,若山高为 千米,
千米,(1)船的航行速度是每小时多少千米?
(2)若该船继续航行
 分钟到达
分钟到达 处,问此时山顶位于
处,问此时山顶位于 处的南偏东什么方向?
处的南偏东什么方向?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知奇函数f(x)满足f(x+2)=f(x﹣2),当x∈(0,1)时,f(x)=3x , 则f(
 )= .
)= .
相关试题

