【题目】甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
参考答案:
【答案】
(1)解:记甲、乙两人同时参加A岗位服务为事件EA,
总事件数是从5个人中选2个作为一组,同其他3人共4个元素在四个位置进行排列C52A44.
满足条件的事件数是A33,
那么 ![]() ,
,
即甲、乙两人同时参加A岗位服务的概率是 ![]() .
.
(2)解:记甲、乙两人同时参加同一岗位服务为事件E,
满足条件的事件数是A44,
那么 ![]() ,
,
∴甲、乙两人不在同一岗位服务的概率是 ![]() .
.
(3)解:随机变量ξ可能取的值为1,2.事件“ξ=2”是指有两人同时参加A岗位服务,
则 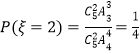 .
.
∴ ![]() ,ξ的分布列是
,ξ的分布列是
ξ | 1 | 2 |
P |
|
|
【解析】(1)甲、乙两人同时参加A岗位服务,则另外三个人在B、C、D三个位置进行全排列,所有的事件数是从5个人中选2个作为一组,同其他3人共4个元素在四个位置进行排列.(2)总事件数同第一问一样,甲、乙两人不在同一个岗位服务的对立事件是甲、乙两人同时参加同一岗位服务,即甲、乙两人作为一个元素同其他三个元素进行全排列.(3)五名志愿者中参加A岗位服务的人数ξ可能的取值是1、2,ξ=2”是指有两人同时参加A岗位服务,同第一问类似做出结果.写出分布列.
【考点精析】利用离散型随机变量及其分布列对题目进行判断即可得到答案,需要熟知在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4.
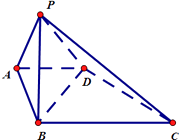
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
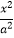 +
+ 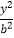 =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ 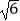 与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
(1)求椭圆C的方程;
(2)已知A为椭圆C上的左顶点,直线∫过右焦点F2与椭圆C交于M,N两点,若AM,AN的斜率k1 , k2满足k1+
k2=﹣ ,求直线MN的方程.
,求直线MN的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx﹣
 (a>0),g(x)=4x+
(a>0),g(x)=4x+ 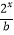 +
+  ,且y=f(x+
,且y=f(x+ 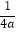 )为偶函数.设集合A={x|t﹣1≤x≤t+1}.
)为偶函数.设集合A={x|t﹣1≤x≤t+1}.
(1)若t=﹣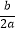 ,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
(2)若对任意的实数t,总存在x1 , x2∈A,使得|f(x1)﹣f(x2)|≥g(x)对x∈[0,1]恒成立,试求a的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处有公共切线,求a,b的值;
(2)当a=3,b=﹣9时,函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设点
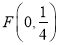 ,动圆
,动圆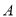 经过点
经过点 且和直线
且和直线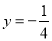 相切,记动圆的圆心
相切,记动圆的圆心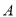 的轨迹为曲线
的轨迹为曲线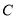 .
. (1)求曲线
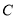 的方程;
的方程;(2)设曲线
 上一点
上一点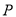 的横坐标为
的横坐标为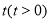 ,过
,过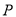 的直线交
的直线交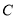 于一点
于一点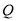 ,交
,交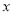 轴于点
轴于点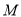 ,过点
,过点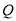 作
作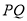 的垂线交
的垂线交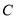 于另一点
于另一点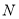 ,若
,若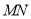 是
是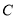 的切线,求
的切线,求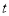 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆Q过定点F(0,﹣1),且与直线y=1相切;椭圆N的对称轴为坐标轴,中心为坐标原点O,F是其一个焦点,又点(0,2)在椭圆N上.
(1)求动圆圆心Q的轨迹M的方程和椭圆N的方程;
(2)过点(0,﹣4)作直线l交轨迹M于A,B两点,连结OA,OB,射线OA,OB交椭圆N于C,D两点,求△OCD面积的最小值.
(3)附加题:过椭圆N上一动点P作圆x2+(y﹣1)2=1的两条切线,切点分别为G,H,求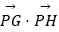 的取值范围.
的取值范围.
相关试题

