【题目】设点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且和直线
且和直线![]() 相切,记动圆的圆心
相切,记动圆的圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 上一点
上一点![]() 的横坐标为
的横坐标为![]() ,过
,过![]() 的直线交
的直线交![]() 于一点
于一点![]() ,交
,交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于另一点
于另一点![]() ,若
,若![]() 是
是![]() 的切线,求
的切线,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)先利用抛物线的定义判定动点轨迹是一个抛物线,再利用待定系数法求出抛物线的方程;(2)设出直线方程,联立直线和抛物线的方程,得到关于![]() 的一元二次方程,利用根与系数的关系和导数的几何意义进行求解.
的一元二次方程,利用根与系数的关系和导数的几何意义进行求解.
试题解析:(1)过点![]() 作直线
作直线![]() 垂直于直线
垂直于直线![]() 于点
于点![]() ,由题意得
,由题意得![]() ,所以动点
,所以动点![]() 的轨迹是以
的轨迹是以![]() 为焦点,直线
为焦点,直线![]() 为准线的抛物线.所以抛物线
为准线的抛物线.所以抛物线![]() 得方程为
得方程为![]() .
.
(2)由题意知,过点![]() 的直线
的直线![]() 斜率存在且不为
斜率存在且不为![]() ,设其为
,设其为![]() ,则
,则![]() ,当
,当![]() ,则
,则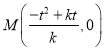 .联立方程
.联立方程![]() ,整理得:
,整理得: ![]() .即
.即![]() ,解得
,解得![]() 或
或![]() ,
, ![]() ,而
,而![]() ,所以直线
,所以直线![]() 斜率为
斜率为![]() ,
, ![]() ,联立方程
,联立方程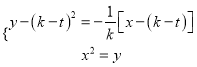 ,整理得:
,整理得: ![]() ,即
,即![]() ,解得
,解得![]() ,或
,或![]() .
.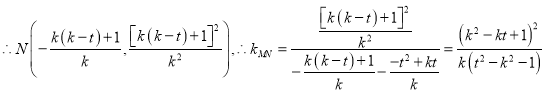 .
.
而抛物线在点![]() 的切线斜率,
的切线斜率, ![]()
![]() ,
, ![]() 是抛物线的切线,
是抛物线的切线, 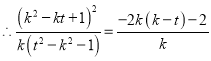 ,整理得
,整理得![]() ,解得
,解得![]() (舍去),或
(舍去),或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义在R上的偶函数f(x),对任意x1 , x2∈[0,+∞)(x1≠x2),有
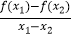 <0,则( )
<0,则( )
A.f(3)<f(﹣2)<f(1)
B.f(1)<f(﹣2)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(1)<f(﹣2) -
科目: 来源: 题型:
查看答案和解析>>【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)﹣g(x)=ex , 则有( )
A.f(2)<f(3)<g(0)
B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3)
D.g(0)<f(2)<f(3) -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆与双曲线有相同的焦点
 ,
, ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为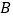 ,直线
,直线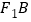 与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为
与双曲线的一条渐近线平行,若椭圆于双曲线的离心率分别为 ,
, ,则
,则 的最小值为__________.
的最小值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
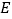 :
: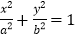 (
(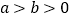 )的右焦点为
)的右焦点为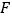 ,短轴的一个端点为
,短轴的一个端点为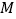 ,直线
,直线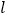 :
: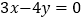 交椭圆
交椭圆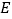 于
于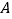 ,
,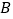 两点,若
两点,若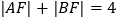 ,点
,点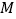 到直线
到直线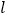 的距离等于
的距离等于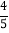 ,则椭圆
,则椭圆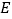 的焦距长为()
的焦距长为()A.
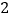 B.
B. 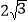 C.
C. 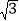 D.
D. 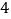
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=ax3+bx+
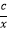 +2,满足f(﹣3)=﹣2015,则f(3)的值为 .
+2,满足f(﹣3)=﹣2015,则f(3)的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
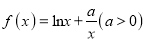 .
.(Ⅰ) 若函数
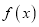 有零点, 求实数
有零点, 求实数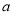 的取值范围;
的取值范围;(Ⅱ) 证明:当
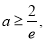 时,
时, 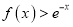
相关试题

