【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0),直线y=x+
=1(a>b>0),直线y=x+ ![]() 与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
与以原点为圆心,以椭圆C的短半轴为半径的圆相切,F1 , F2为其左右焦点,P为椭圆C上的任意一点,△F1PF2的重心为G,内心为I,且IG∥F1F2 .
(1)求椭圆C的方程;
(2)已知A为椭圆C上的左顶点,直线∫过右焦点F2与椭圆C交于M,N两点,若AM,AN的斜率k1 , k2满足k1+
k2=﹣ ![]() ,求直线MN的方程.
,求直线MN的方程.
参考答案:
【答案】
(1)解:设P(x0,y0),I(x1,y1),则G( ![]() ).
).
又IG∥F1F2, ![]() ,|F1F2|=2c,
,|F1F2|=2c,
∴ ![]() =
= ![]() |F1F2||y0|=
|F1F2||y0|= ![]() .
.
∴2c= ![]() ,故a=2c.
,故a=2c.
又直线y=x+ ![]() 与以原点为圆心,以椭圆C的短半轴为半径的圆相切,
与以原点为圆心,以椭圆C的短半轴为半径的圆相切,
∴b= ![]() =
= ![]() ,
,
∴a=2,c=1.∴ ![]() .
.
(2)解:若直线l斜率不存在,显然k1+k2=0不合题意;
则直线l的斜率存在.
设直线l为y=k(x﹣1),直线l和椭圆交于M(x1,y1),N(x2,y2).
将y=k(x﹣1)代入3x2+4y2=12中,得:
(3+4k2)x2﹣8k2x+4k2﹣12=0,
依题意:△=9k2+9>0,
由韦达定理知: 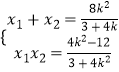 ,
,
又kAM+kAN= ![]() =k(
=k( ![]() )
)
=k[2﹣3( ![]() )],
)],
![]() =
= ![]()
= ![]()
= ![]() ,
,
从而kAM+kAN=k(2﹣3 ![]() )=﹣
)=﹣ ![]() ,
,
解得k=2,符合△>0.
故所求直线MN的方程为:y=2(x﹣1)
【解析】(1)设P(x0 , y0),I(x1 , y1),则G( ![]() ),由已知条件推导出a=2c,b=
),由已知条件推导出a=2c,b= ![]() =
= ![]() 由此能求出椭圆方程.(2)设直线l为y=k(x﹣1),直线l和椭圆交于M(x1 , y1),N(x2 , y2).将y=k(x﹣1)代入3x2+4y2=12中,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用韦达定理能求出直线MN的方程.
由此能求出椭圆方程.(2)设直线l为y=k(x﹣1),直线l和椭圆交于M(x1 , y1),N(x2 , y2).将y=k(x﹣1)代入3x2+4y2=12中,得(3+4k2)x2﹣8k2x+4k2﹣12=0,由此利用韦达定理能求出直线MN的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x|2x﹣a|,g(x)=
 (a∈R),若0<a<12,且对任意t∈[3,5],方程f(x)=g(t)在x∈[3,5]总存在两不相等的实数根,求a的取值范围 .
(a∈R),若0<a<12,且对任意t∈[3,5],方程f(x)=g(t)在x∈[3,5]总存在两不相等的实数根,求a的取值范围 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块长方体木料中,已知AB=BC=4,AA1=1,设E为底面ABCD的中心,且
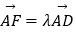 (0≤λ≤
(0≤λ≤  ),则该长方体中经过点A1、E、F的截面面积的最小值为
),则该长方体中经过点A1、E、F的截面面积的最小值为 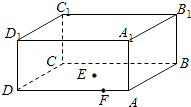
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,AB⊥BC侧面PAB⊥底面ABCD,PA=AD=AB=2,BC=4.
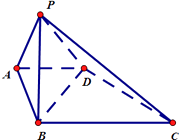
(1)若PB中点为E.求证:AE∥平面PCD;
(2)若∠PAB=60°,求直线BD与平面PCD所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+bx﹣
 (a>0),g(x)=4x+
(a>0),g(x)=4x+ 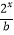 +
+  ,且y=f(x+
,且y=f(x+ 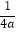 )为偶函数.设集合A={x|t﹣1≤x≤t+1}.
)为偶函数.设集合A={x|t﹣1≤x≤t+1}.
(1)若t=﹣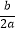 ,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
,记f(x)在A上的最大值与最小值分别为M,N,求M﹣N;
(2)若对任意的实数t,总存在x1 , x2∈A,使得|f(x1)﹣f(x2)|≥g(x)对x∈[0,1]恒成立,试求a的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一个岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ax2+1(a>0),g(x)=x3+bx.
(1)若曲线y=f(x)与曲线y=g(x)在它们的交点(1,c)处有公共切线,求a,b的值;
(2)当a=3,b=﹣9时,函数f(x)+g(x)在区间[k,2]上的最大值为28,求k的取值范围.
相关试题

