【题目】抛物线![]() 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在![]() 轴正半轴上,准线
轴正半轴上,准线![]() 与圆
与圆![]() 相切.
相切.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和抛物线
和抛物线![]() 交于点
交于点![]() ,命题
,命题![]() :“若直线
:“若直线![]() 过定点(0,1),则
过定点(0,1),则 ![]() ”,
”,
请判断命题![]() 的真假,并证明.
的真假,并证明.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)命题P为真命题
(Ⅱ)命题P为真命题
【解析】
试题分析:(Ⅰ)设抛物线C的方程为:x2=2py,p>0,由已知条件得圆心(0,0)到直线l的距离![]() ,由此能求出抛物线线C的方程;(Ⅱ)设直线m:y=kx+1,交点A
,由此能求出抛物线线C的方程;(Ⅱ)设直线m:y=kx+1,交点A ![]() ,B
,B ![]() 联立抛物线C的方程
联立抛物线C的方程![]() ,得x2-4kx-4=0,△=16k2+16>0恒成立,由此利用韦达定理能证明命题P为真命题
,得x2-4kx-4=0,△=16k2+16>0恒成立,由此利用韦达定理能证明命题P为真命题
试题解析:(Ⅰ)依题意,可设抛物线C的方程为:![]() ,
,![]()
其准线![]() 的方程为:
的方程为:![]()
∵准线![]() 圆
圆![]() 相切 ∴
相切 ∴![]() 解得p=4
解得p=4
故抛物线线C的方程为:![]() ………….…5分
………….…5分
(Ⅱ)命题p为真命题 ……………………………………6分
直线m和抛物线C交于A,B且过定点(0,1),
故所以直线m的斜率k一定存在,………………………7分
设直线m:![]() ,交点
,交点![]()
![]() ,
,![]() ,联立抛物线C的方程,
,联立抛物线C的方程,![]()
得![]() ,
,![]() 恒成立,………8分
恒成立,………8分
由韦达定理得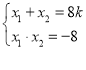 ………………………………………9分
………………………………………9分
![]()
![]() =
=![]()
![]()
∴命题P为真命题.………………………………………12分.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
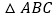 中,边
中,边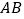 ,
,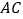 所在直线的方程分别为
所在直线的方程分别为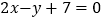 ,
, ,已知
,已知 是
是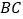 边上一点.
边上一点.(1)若
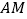 为
为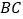 边上的高,求直线
边上的高,求直线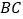 的方程;
的方程;(2)若
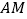 为
为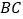 边的中线,求
边的中线,求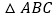 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
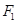 、
、 分别为椭圆
分别为椭圆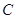 :
: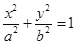
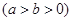 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆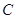 上的点
上的点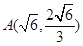 到
到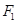 、
、 两点的距离之和等于6,写出椭圆
两点的距离之和等于6,写出椭圆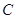 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点M的轨迹方程.
的中点M的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某课题进行研究,用分层抽样方法从三所高校
 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)高校
相关人数
抽取人数
A
18
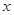
B
36
2
C
54
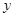
(Ⅰ)求
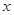 ,
,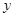 ;
;(Ⅱ)若从高校
 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校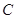 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是________.(填序号)
① 若a⊥b,a⊥α,则b∥α;② 若a∥α,α⊥β,则a⊥β;
③ 若a⊥β,α⊥β,则a∥α;④ 若a⊥b,a⊥α,b⊥β,则α⊥β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,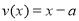 ,
,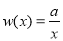 ,三个函数的定义域均为集合
,三个函数的定义域均为集合 .
.(1)若
 ,试判断集合
,试判断集合 与
与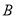 的关系,并说明理由;
的关系,并说明理由;(2)记
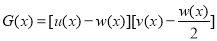 ,是否存在
,是否存在 ,使得对任意的实数
,使得对任意的实数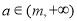 ,函数
,函数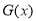 有且仅有两个零点?若存在,求出满足条件的最小正整数
有且仅有两个零点?若存在,求出满足条件的最小正整数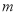 ;若不存在,说明理由.(以下数据供参考:
;若不存在,说明理由.(以下数据供参考: ,
,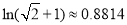 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C的标准方程是

(Ⅰ)求它的焦点坐标和准线方程;
(Ⅱ)直线
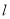 过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
相关试题

