【题目】在![]() 中,边
中,边![]() ,
,![]() 所在直线的方程分别为
所在直线的方程分别为![]() ,
,![]() ,已知
,已知![]() 是
是![]() 边上一点.
边上一点.
(1)若![]() 为
为![]() 边上的高,求直线
边上的高,求直线![]() 的方程;
的方程;
(2)若![]() 为
为![]() 边的中线,求
边的中线,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() (2)6
(2)6
【解析】试题分析:
(1)利用题意首先求得BC的斜率,然后由点斜式可得直线![]() 的方程为
的方程为![]() ;
;
(2)由题意可得三角形的高为![]() ,结合几何关系可得
,结合几何关系可得![]() 的面积为6.
的面积为6.
试题解析:
(1)由![]() 解得
解得![]() ,即
,即![]() ,分
,分
又![]() ,所以
,所以![]() ,
,
因为![]() 为
为![]() 边上的高,所以
边上的高,所以![]() ,
,
![]() 为
为![]() 边上一点,所以
边上一点,所以![]()
![]() ,
,
所以直线![]() 的方程为
的方程为![]() .
.
(2)法一:设点![]() 的坐标为
的坐标为![]() ,由
,由![]() 为
为![]() 的中点,得点
的中点,得点![]() 的坐标为
的坐标为![]() ,
,
又点![]() 与点
与点![]() 分别在直线
分别在直线![]() 和
和![]() 上,
上,
所以![]() ,解得
,解得![]() ,
,
所以点![]() 的坐标为
的坐标为![]() ,
,
由(1)得![]() ,又
,又![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,
,
所以点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
又![]() ,
,
所以![]() ,
,
又![]() 为
为![]() 的中点
的中点
所以![]() .
.
法二:(上同法一)
点![]() 的坐标为
的坐标为![]() ,
,
又![]() 为
为![]() 上一点,
上一点,
所以直线![]() 的方程为
的方程为![]() .
.
由(1)知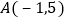 ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离
![]() ,
,
又![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,
所以![]() .
.
法三:若直线![]() 的斜率不存在,即
的斜率不存在,即![]() 的方程为
的方程为![]() ,
,
由![]() 解得
解得![]() ,
,
即![]() 的坐标为
的坐标为![]() ,同理可得
,同理可得![]() 的坐标为
的坐标为![]() ,
,
而![]() ,
, ![]() 不是
不是![]() 的中点,所以直线
的中点,所以直线![]() 的斜率存在.
的斜率存在.
设直线![]() 的方程为
的方程为![]()
由![]() 解得
解得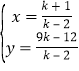 ,即
,即![]() 的坐标为
的坐标为![]() 同理可得
同理可得![]() 的坐标为
的坐标为![]() ,
,![]() 为
为![]() 的中点
的中点
所以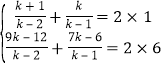 解得
解得![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即为
,即为![]() .
.
(下同法二)
法四:求![]() 正弦值即
正弦值即![]() ,
,![]() 长用面积公式(略).
长用面积公式(略).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 (
( ),焦点
),焦点 到准线的距离为
到准线的距离为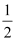 ,过点
,过点
 作直线
作直线 交抛物线
交抛物线 于点
于点 (点
(点 在第一象限).
在第一象限).(Ⅰ)若点
 焦点
焦点 重合,且弦长
重合,且弦长 ,求直线
,求直线 的方程;
的方程; (Ⅱ)若点
 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线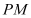 交x轴于点
交x轴于点 ,且
,且 ,求证:点B的坐标是
,求证:点B的坐标是 ,并求点
,并求点 到直线
到直线 的距离
的距离 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,点
的焦点重合,点 在
在 上
上(Ⅰ)求
 的方程;
的方程; (Ⅱ)直线
 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴, 与
与 有两个交点
有两个交点 ,线段
,线段 的中点为
的中点为 ,证明:
,证明: 的斜率与直线
的斜率与直线 的斜率的乘积为定值.
的斜率的乘积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
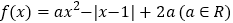 .
.(1)当
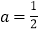 时,解不等式
时,解不等式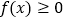 ;
;(2)若
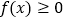 恒成立,求
恒成立,求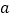 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
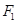 、
、 分别为椭圆
分别为椭圆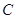 :
: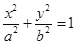
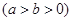 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆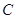 上的点
上的点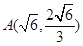 到
到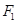 、
、 两点的距离之和等于6,写出椭圆
两点的距离之和等于6,写出椭圆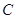 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点M的轨迹方程.
的中点M的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某课题进行研究,用分层抽样方法从三所高校
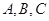 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)高校
相关人数
抽取人数
A
18
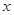
B
36
2
C
54
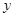
(Ⅰ)求
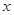 ,
,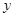 ;
;(Ⅱ)若从高校
 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校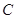 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在 轴正半轴上,准线
轴正半轴上,准线 与圆
与圆 相切.
相切.(Ⅰ)求抛物线
 的方程;
的方程; (Ⅱ)已知直线
 和抛物线
和抛物线 交于点
交于点 ,命题
,命题 :“若直线
:“若直线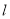 过定点(0,1),则
过定点(0,1),则  ”,
”,请判断命题
 的真假,并证明.
的真假,并证明.
相关试题

