【题目】已知抛物线C的标准方程是![]()
(Ⅰ)求它的焦点坐标和准线方程;
(Ⅱ)直线![]() 过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
过已知抛物线C的焦点且倾斜角为45°,且与抛物线的交点为A、B,求线段AB的长度.
参考答案:
【答案】(Ⅰ)焦点为F(![]() ,0),准线方程:
,0),准线方程:![]() (Ⅱ)12
(Ⅱ)12
【解析】
试题分析:(1)抛物线的标准方程是![]() ,焦点在x轴上,开口向右,2p=6,即可求出抛物线的焦点坐标和准线方程;(2)先根据题意给出直线l的方程,代入抛物线,求出两交点的横坐标的和,然后利用焦半径公式求解即可
,焦点在x轴上,开口向右,2p=6,即可求出抛物线的焦点坐标和准线方程;(2)先根据题意给出直线l的方程,代入抛物线,求出两交点的横坐标的和,然后利用焦半径公式求解即可
试题解析:(1)抛物线的标准方程是![]() ,焦点在x轴上,开口向右,
,焦点在x轴上,开口向右,![]() ,∴焦点为F(
,∴焦点为F(![]() ,0),准线方程:
,0),准线方程:![]() ,……………………4分
,……………………4分
(2)∵直线![]() 过已知抛物线的焦点且倾斜角为45°,
过已知抛物线的焦点且倾斜角为45°,
∴直线![]() 的方程为
的方程为![]() ,………………………………………5分
,………………………………………5分
代入抛物线![]() ,化简得
,化简得![]() ………………7分
………………7分
设![]() ,
,![]() ,则
,则![]() ,
,
所以![]()
故所求的弦长为12.…………………………………………………10分
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在 轴正半轴上,准线
轴正半轴上,准线 与圆
与圆 相切.
相切.(Ⅰ)求抛物线
 的方程;
的方程; (Ⅱ)已知直线
 和抛物线
和抛物线 交于点
交于点 ,命题
,命题 :“若直线
:“若直线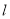 过定点(0,1),则
过定点(0,1),则  ”,
”,请判断命题
 的真假,并证明.
的真假,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是________.(填序号)
① 若a⊥b,a⊥α,则b∥α;② 若a∥α,α⊥β,则a⊥β;
③ 若a⊥β,α⊥β,则a∥α;④ 若a⊥b,a⊥α,b⊥β,则α⊥β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,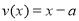 ,
,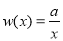 ,三个函数的定义域均为集合
,三个函数的定义域均为集合 .
.(1)若
 ,试判断集合
,试判断集合 与
与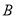 的关系,并说明理由;
的关系,并说明理由;(2)记
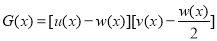 ,是否存在
,是否存在 ,使得对任意的实数
,使得对任意的实数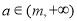 ,函数
,函数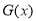 有且仅有两个零点?若存在,求出满足条件的最小正整数
有且仅有两个零点?若存在,求出满足条件的最小正整数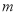 ;若不存在,说明理由.(以下数据供参考:
;若不存在,说明理由.(以下数据供参考: ,
,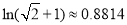 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组
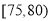 ,第二组
,第二组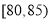 ,第三组
,第三组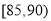 ,第四组
,第四组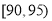 ,第五组
,第五组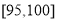 ,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
,如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.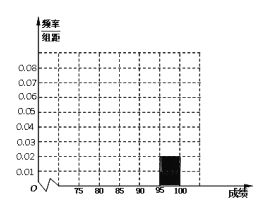
(I)请在图中补全频率直方图;
(II)若
 大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率.
大学决定在成绩高的第4,5组中用分层抽样的方法抽取6名学生,并且分成2组,每组3人进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
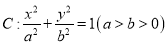 的左、右焦点分别为
的左、右焦点分别为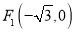 、
、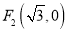 ,椭圆上的点
,椭圆上的点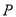 满足
满足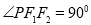 ,且
,且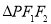 的面积为
的面积为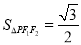 .
.(1)求椭圆
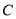 的方程;
的方程;(2)设椭圆
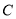 的左、右顶点分别为
的左、右顶点分别为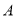 、
、 ,过点
,过点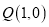 的动直线
的动直线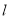 与椭圆
与椭圆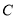 相交于
相交于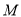 、
、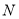 两点,直线
两点,直线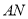 与直线
与直线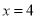 的交点为
的交点为 ,证明:点
,证明:点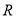 总在直线
总在直线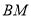 上.
上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABCA1B1C1中, CC1⊥平面ABC, AC⊥BC, AB1的中点为D,B1C∩BC1=E. 求证:
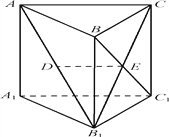
(1)DE∥平面AA1C1C;
(2)AC⊥平面BCC1B1.
相关试题

