【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)利用分层抽样的特点(等比例抽样)进行求解;(Ⅱ)利用列举法得到所有和符合题意的基本事件和基本事件个数,再利用古典概型的概率公式进行求解.
试题解析:(Ⅰ)由题意可得![]() ,∴
,∴![]() ,
,![]() .
.
(Ⅱ)记从高校![]() 抽取的2人为
抽取的2人为![]() ,从高校
,从高校![]() 抽取的3人为
抽取的3人为![]() ,则从高校
,则从高校![]() 抽取的5人中选2人作专题发言的基本事件有
抽取的5人中选2人作专题发言的基本事件有![]() ,共10种.
,共10种.
设选中的2人都来自高校![]() 的事件为
的事件为![]() ,则
,则![]() 包含的基本事件有
包含的基本事件有![]() ,共3种,
,共3种,
因此![]() ,故选中的2人都来自高校
,故选中的2人都来自高校![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
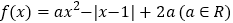 .
.(1)当
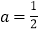 时,解不等式
时,解不等式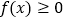 ;
;(2)若
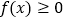 恒成立,求
恒成立,求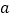 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
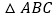 中,边
中,边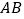 ,
,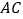 所在直线的方程分别为
所在直线的方程分别为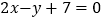 ,
, ,已知
,已知 是
是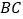 边上一点.
边上一点.(1)若
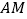 为
为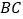 边上的高,求直线
边上的高,求直线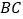 的方程;
的方程;(2)若
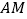 为
为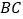 边的中线,求
边的中线,求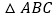 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
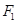 、
、 分别为椭圆
分别为椭圆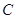 :
: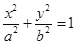
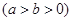 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)若椭圆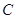 上的点
上的点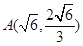 到
到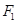 、
、 两点的距离之和等于6,写出椭圆
两点的距离之和等于6,写出椭圆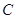 的方程和焦点坐标;
的方程和焦点坐标;
(Ⅱ)设点 是(1)中所得椭圆上的动点,求线段
是(1)中所得椭圆上的动点,求线段 的中点M的轨迹方程.
的中点M的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 的顶点为坐标原点O,焦点F在
的顶点为坐标原点O,焦点F在 轴正半轴上,准线
轴正半轴上,准线 与圆
与圆 相切.
相切.(Ⅰ)求抛物线
 的方程;
的方程; (Ⅱ)已知直线
 和抛物线
和抛物线 交于点
交于点 ,命题
,命题 :“若直线
:“若直线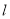 过定点(0,1),则
过定点(0,1),则  ”,
”,请判断命题
 的真假,并证明.
的真假,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是不同的直线,α,β是不同的平面,则下列四个命题中正确的是________.(填序号)
① 若a⊥b,a⊥α,则b∥α;② 若a∥α,α⊥β,则a⊥β;
③ 若a⊥β,α⊥β,则a∥α;④ 若a⊥b,a⊥α,b⊥β,则α⊥β.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,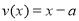 ,
,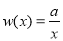 ,三个函数的定义域均为集合
,三个函数的定义域均为集合 .
.(1)若
 ,试判断集合
,试判断集合 与
与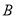 的关系,并说明理由;
的关系,并说明理由;(2)记
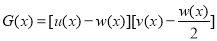 ,是否存在
,是否存在 ,使得对任意的实数
,使得对任意的实数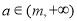 ,函数
,函数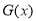 有且仅有两个零点?若存在,求出满足条件的最小正整数
有且仅有两个零点?若存在,求出满足条件的最小正整数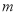 ;若不存在,说明理由.(以下数据供参考:
;若不存在,说明理由.(以下数据供参考: ,
,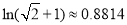 )
)
相关试题

