【题目】(本小题12分)根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
]
组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)年该居民区PM2.5年平均浓度为
;(Ⅱ)年该居民区PM2.5年平均浓度为![]() 微克/立方米.去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
微克/立方米.去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
【解析】
试题分析:(Ⅰ)将从这5天中任意抽取2天所包含的所有基本事件一一例举,再将抽取的2天恰有一天PM2.5的24小时平均浓度超过75微克/立方米的所包含的基本事件一一例举,根据古典概型概率公式可求得所求.(Ⅱ)每组的中点与本组频率乘积之和即为所求的PM2.5的年平均浓度,若大于35不符合环境空气质量标准,否则即符合环境空气质量标准.
试题解析:解:(Ⅰ)设PM2.5的24小时平均浓度在![]() 内的三天记为
内的三天记为![]() ,PM2.5的24小时平均浓度在
,PM2.5的24小时平均浓度在![]() 内的两天记为
内的两天记为![]() .
.
所以5天任取2天的情况有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共10种.
共10种.
其中符合条件的有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种.
共6种.
所以所求的概率![]() .
.
(Ⅱ)去年该居民区PM2.5年平均浓度为:
![]() (微克/立方米).
(微克/立方米).
因为![]() ,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
,所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准,故该居民区的环境需要改进.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大,最大月收益是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
 其中
其中 ,集合
,集合 .
.(1)若
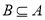 ,求实数
,求实数 的取值范围;
的取值范围;(2)若
 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
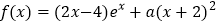 (
(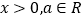 ,
,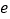 是自然对数的底数).
是自然对数的底数).(1)若
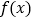 是
是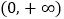 上的单调递增函数,求实数
上的单调递增函数,求实数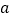 的取值范围;
的取值范围;(2)当
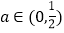 时,证明:函数
时,证明:函数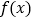 有最小值,并求函数
有最小值,并求函数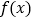 最小值的取值范围.
最小值的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是偶函数.
是偶函数.(1)求
 的值;
的值;(2)若函数
 的图象与直线
的图象与直线 没有交点,求b的取值范围;
没有交点,求b的取值范围;(3)设
 ,若函数
,若函数 与
与 的图象有且只有一个公共点,求实数a的取值范围.
的图象有且只有一个公共点,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
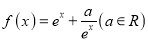 是定义在R上的奇函数,其中
是定义在R上的奇函数,其中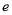 为自然对数的底数.
为自然对数的底数.(1)求实数
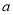 的值;
的值;(2)若存在
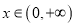 ,使得不等式
,使得不等式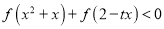 成立,求实数
成立,求实数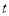 的取值范围;
的取值范围;(3)若函数
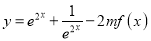 在
在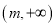 上不存在最值,求实数
上不存在最值,求实数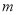 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义区间(a,b),[a,b),(a,b],[a,b]的长度均为
 ,多个区间并集的长度为各区间长度之和,例如,(1,2)
,多个区间并集的长度为各区间长度之和,例如,(1,2)  [3,5)的长度d=(2-1)+(5-3)=3. 用[x]表示不超过x的最大整数,记{x}=x-[x],其中
[3,5)的长度d=(2-1)+(5-3)=3. 用[x]表示不超过x的最大整数,记{x}=x-[x],其中 .设
.设 ,
,  ,当
,当 时,不等式
时,不等式 解集区间的长度为
解集区间的长度为 ,则
,则 的值为_______.
的值为_______.
相关试题

