【题目】已知抛物线过点(2,1)且关于![]() 轴对称.
轴对称.
(1)求抛物线![]() 的方程;
的方程;
(2)已知圆过定点![]() ,圆心
,圆心![]() 在抛物线
在抛物线![]() 上运动,且圆
上运动,且圆![]() 与
与![]() 轴交于
轴交于![]() 两点,设
两点,设![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 时最大值为
时最大值为![]() .
.
【解析】试题分析:(1)设出抛物线的标准形式,代入已知点坐标即可求解;
(2)(2)设M(a,b),则a2=4b.半径R=![]() ,可得 M的方程为(x-a)2+(y-b)2=a2+(b-2)2,令y=0,解得x,可得A,B.利用两点之间的距离公式可得:l1,l2.代入利用基本不等式的性质即可得出.
,可得 M的方程为(x-a)2+(y-b)2=a2+(b-2)2,令y=0,解得x,可得A,B.利用两点之间的距离公式可得:l1,l2.代入利用基本不等式的性质即可得出.
试题解析:
(1)设抛物线方程为: ![]()
代入点(2,1),解得p=2,所以有: ![]() ;
;
(2)设圆M的圆心坐标为![]() ,则
,则![]() ①
①
圆M的半径为![]()
圆M的方程为![]()
令![]() ,则
,则![]()
整理得![]() ②
②
由①②解得![]() ,
,
不妨设![]() ,
,
所以![]() ,
,![]()
所以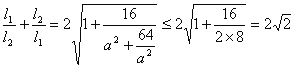 ,
,
当且仅当![]() ,即
,即![]() 时取等号,
时取等号,
当![]() 时,
时,![]() ,
,
综上可知,当![]() 时,所求最大值为
时,所求最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
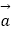 =(cosα,sinα),
=(cosα,sinα), 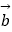 =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若|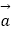 ﹣
﹣ 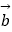 |=
|= 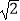 ,求证:
,求证: 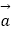 ⊥
⊥ 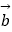 ;
;
(2)设c=(0,1),若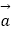 +
+ 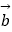 =c,求α,β的值.
=c,求α,β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
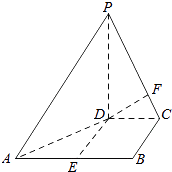
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,
,  ,
,  .等 差数列
.等 差数列 中,
中,  ,且公差
,且公差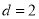 .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)是否存在正整数
 ,使得
,使得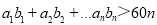 ?.若存在,求出
?.若存在,求出 的最小值;若 不存在,请说明理由.
的最小值;若 不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆
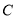 的极坐标方程为:
的极坐标方程为: 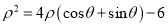 .若以极点
.若以极点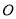 为原点,极轴所在直线为
为原点,极轴所在直线为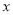 轴建立平面直角坐标系.
轴建立平面直角坐标系.(Ⅰ)求圆
 的直角坐标方程及其参数方程;
的直角坐标方程及其参数方程;(Ⅱ)在直角坐标系中,点
 是圆
是圆 上动点,求
上动点,求 的最大值,并求出此时
的最大值,并求出此时点
 的直角坐标.
的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】(选修4-4 坐标系与参数方程) 以平面直角坐标系的原点为极点,
 轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为
轴的正半轴为极轴建立极坐标系,设曲线C的参数方程为 (
( 是参数),直线
是参数),直线 的极坐标方程为
的极坐标方程为 .
.(1)求直线
 的直角坐标方程和曲线C的普通方程;
的直角坐标方程和曲线C的普通方程;(2)设点P为曲线C上任意一点,求点P到直线
 的距离的最大值.
的距离的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2+2x+a=0上存在两点关于直线l:mx+y+1=0对称. (Ⅰ)求m的值;
(Ⅱ)直线l与圆C交于A,B两点,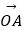
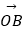 =﹣3(O为坐标原点),求圆C的方程.
=﹣3(O为坐标原点),求圆C的方程.
相关试题

