【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°. 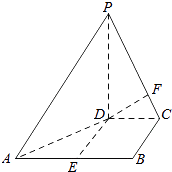
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离.
参考答案:
【答案】
(1)证明:因为PD⊥平面ABCD,BC平面ABCD,所以PD⊥BC.
由∠BCD=90°,得CD⊥BC,
又PD∩DC=D,PD、DC平面PCD,
所以BC⊥平面PCD.
因为PC平面PCD,故PC⊥BC.
(2)解:(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等.
又点A到平面PBC的距离等于E到平面PBC的距离的2倍.
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F.
易知DF= ![]() ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于 ![]() .
.
(方法二)等体积法:连接AC.设点A到平面PBC的距离为h.
因为AB∥DC,∠BCD=90°,所以∠ABC=90°.
从而AB=2,BC=1,得△ABC的面积S△ABC=1.
由PD⊥平面ABCD及PD=1,得三棱锥P﹣ABC的体积 ![]() .
.
因为PD⊥平面ABCD,DC平面ABCD,所以PD⊥DC.
又PD=DC=1,所以 ![]() .
.
由PC⊥BC,BC=1,得△PBC的面积 ![]() .
.
由VA﹣PBC=VP﹣ABC, ![]() ,得
,得 ![]() ,
,
故点A到平面PBC的距离等于 ![]() .
.
【解析】(1),要证明PC⊥BC,可以转化为证明BC垂直于PC所在的平面,由PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,容易证明BC⊥平面PCD,从而得证;(2),有两种方法可以求点A到平面PBC的距离: 方法一,注意到第一问证明的结论,取AB的中点E,容易证明DE∥平面PBC,点D、E到平面PBC的距离相等,而A到平面PBC的距离等于E到平面PBC的距离的2倍,由第一问证明的结论知平面PBC⊥平面PCD,交线是PC,所以只求D到PC的距离即可,在等腰直角三角形PDC中易求;
方法二,等体积法:连接AC,则三棱锥P﹣ACB与三棱锥A﹣PBC体积相等,而三棱锥P﹣ACB体积易求,三棱锥A﹣PBC的地面PBC的面积易求,其高即为点A到平面PBC的距离,设为h,则利用体积相等即求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.现从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
产品编号
A1
A2
A3
A4
A5
质量指标
(x , y , z)(1,1,2)
(2,1,1)
(2,2,2)
(1,1,1)
(1,2,1)
产品编号
A6
A7
A8
A9
A10
质量指标
(x , y , z)(1,2,2)
(2,1,1)
(2,2,1)
(1,1,1)
(2,1,2)
(1)利用上表提供的样本数据估计该批产品的一等品率.
(2)在该样品的一等品中,随机抽取2件产品, ①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 中,
中,  分别为两腰上的高、求证:
分别为两腰上的高、求证: 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
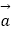 =(cosα,sinα),
=(cosα,sinα), 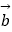 =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若|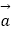 ﹣
﹣ 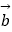 |=
|= 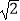 ,求证:
,求证: 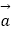 ⊥
⊥ 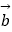 ;
;
(2)设c=(0,1),若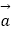 +
+ 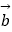 =c,求α,β的值.
=c,求α,β的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 的前
的前 项和为
项和为 ,
,  ,
,  .等 差数列
.等 差数列 中,
中,  ,且公差
,且公差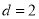 .
.(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)是否存在正整数
 ,使得
,使得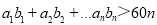 ?.若存在,求出
?.若存在,求出 的最小值;若 不存在,请说明理由.
的最小值;若 不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线过点(2,1)且关于
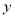 轴对称.
轴对称.(1)求抛物线
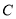 的方程;
的方程;(2)已知圆过定点
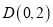 ,圆心
,圆心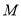 在抛物线
在抛物线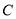 上运动,且圆
上运动,且圆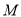 与
与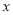 轴交于
轴交于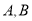 两点,设
两点,设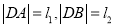 ,求
,求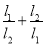 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆
 的极坐标方程为:
的极坐标方程为: 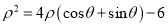 .若以极点
.若以极点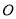 为原点,极轴所在直线为
为原点,极轴所在直线为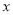 轴建立平面直角坐标系.
轴建立平面直角坐标系.(Ⅰ)求圆
 的直角坐标方程及其参数方程;
的直角坐标方程及其参数方程;(Ⅱ)在直角坐标系中,点
 是圆
是圆 上动点,求
上动点,求 的最大值,并求出此时
的最大值,并求出此时点
 的直角坐标.
的直角坐标.
相关试题

