【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 在棱
在棱![]() 上.
上.
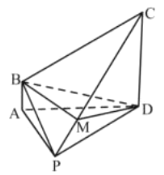
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若直线![]() 平面
平面![]() ,求此时三棱椎
,求此时三棱椎![]() 的体积.
的体积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用正弦定理和三角形的内角和定理证得![]() ,结合
,结合![]() ,利用线面垂直的判定定理证得
,利用线面垂直的判定定理证得![]() 平面
平面![]() ,再由面面垂直的判定定理即可证明;
,再由面面垂直的判定定理即可证明;
(2)如图所示,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,可证明
,可证明![]() ~
~![]() ,
,![]() ,由
,由![]() ,作
,作![]() 于点
于点![]() ,可证
,可证![]() 平面
平面![]() ,代入题中的数据进行计算,即可求出
,代入题中的数据进行计算,即可求出![]() 的体积.
的体积.
(1)证明:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
由正弦定理可得,![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)如图:连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
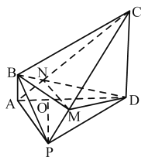
因为直线![]() 平面
平面![]() ,过
,过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
,
由线面平行的性质定理可得,![]() ,
,
在梯形![]() 中,因为
中,因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ~
~![]() ,即
,即![]() ,
,
因为![]() ,所以
,所以![]()
![]()
![]() ,
,
∴![]() ,即
,即![]() ,
,
作![]() 于点
于点![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() ,因为
,因为![]() ,
,
所以![]() 平面
平面![]() ,
,
在![]() 中,由(1)知,
中,由(1)知,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() 即为所求.
即为所求.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
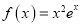
(1)求
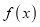 的单调区间;
的单调区间;(2)过点
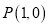 存在几条直线与曲线
存在几条直线与曲线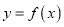 相切,并说明理由;
相切,并说明理由;(3)若
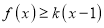 对任意
对任意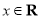 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某市国庆节7天假期的商品房日认购量(单位:套)与日成交量(单位:套)的折线图,则下面结论中正确的是( )
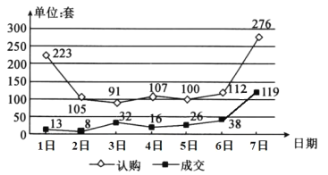
A.日成交量的中位数是16
B.日成交量超过日平均成交量的有1天
C.日认购量与日期是正相关关系
D.日认购量的方差大于日成交量的方差
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
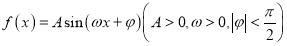 的最大值为
的最大值为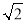 ,其图象相邻两条对称轴之间的距离为
,其图象相邻两条对称轴之间的距离为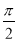 ,且
,且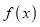 的图象关于点
的图象关于点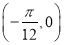 对称,则下列判断正确的是( )
对称,则下列判断正确的是( )A.要得到函数
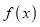 的图象,只需将
的图象,只需将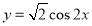 向右平移
向右平移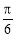 个单位
个单位B.函数
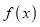 的图象关于直线
的图象关于直线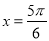 对称
对称C.当
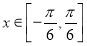 时,函数
时,函数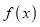 的最小值为
的最小值为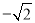
D.函数
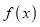 在
在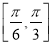 上单调递增
上单调递增 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学就业部从该大学2018年毕业且已就业的大学本科生中随机抽取了100人进行了问卷调查,其中有一项是他们的薪酬,经调查统计,他们的月薪在3000元到10000元之间,根据统计数据得到如下频率分布直方图:
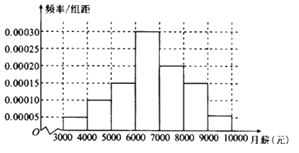
若月薪在区间
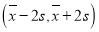 的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中
的左侧,则认为该大学本科生属“就业不理想”的学生,学校将与本人联系,为其提供更好的指导意见.其中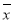 ,
,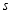 分别是样本平均数和样本标准差,计算得
分别是样本平均数和样本标准差,计算得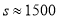 (同一组中的数据用该组区间的中点值作代表)
(同一组中的数据用该组区间的中点值作代表)(1)现该校2018届本科毕业生张静的月薪为3600元,判断张静是否属于“就业不理想”的学生?用样本估计总体,从该校2018届本科毕业生随机选取一人,属于“就业不理想”的概率?
(2)为感谢同学们对调查的支持配合,该校利用分层抽样的方法从样本的前3组中抽出6人,每人赠送一份礼品,并从这6人中再抽取2人,每人赠送新款某手机1部,求获赠手机的2人中恰有1人月薪不超过5000元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
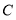 :
: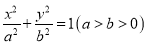 的离心率为
的离心率为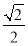 ,且经过点
,且经过点 .
.(1)求椭圆
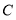 的方程;
的方程;(2)过点
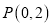 作直线交椭圆
作直线交椭圆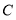 于
于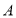 ,
,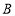 两点,若点
两点,若点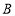 关于
关于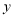 轴的对称点为
轴的对称点为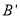 ,证明直线
,证明直线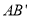 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
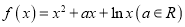 .
.(1)当
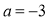 时,求
时,求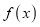 的极值;
的极值;(2)若
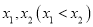 是函数
是函数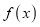 的两个极值点,求
的两个极值点,求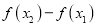 的取值范围.
的取值范围.
相关试题

