【题目】如图,已知点![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,连接
的中点,连接![]() .现将
.现将![]() 沿
沿![]() 折叠至Δ
折叠至Δ![]() 的位置,连接
的位置,连接![]() .记平面
.记平面 ![]() 与平面
与平面 ![]() 的交线为
的交线为![]() ,二面角
,二面角![]() 大小为
大小为![]() .
.


(1)证明: ![]()
(2)证明: ![]()
(3)求平面![]() 与平面
与平面 ![]() 所成锐二面角大小.
所成锐二面角大小.
参考答案:
【答案】(1)见解析;(2)见解析;(3)![]()
![]() .
.
【解析】试题分析:(1)由![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,根据三角形中位线定理可得
的中点,根据三角形中位线定理可得![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形
,再利用线面平行的性质定理可得结论;(2)由三角形中位线定理以可判定四边形![]() 平行四边形,进而可得四边形
平行四边形,进而可得四边形![]() 为菱形,于是可得
为菱形,于是可得![]() ,
, ![]() ,
,![]()
![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得结论;(3)作
,从而根据面面垂直的判定定理可得结论;(3)作![]() 于
于![]() 交
交![]() 于
于![]() ,可知
,可知![]() 是
是![]() 的中点,折叠后角
的中点,折叠后角![]() 是二面角
是二面角![]() 的平面角,可证明等腰
的平面角,可证明等腰![]() 的底角
的底角![]() 是平面
是平面![]() 与平面
与平面![]() 所成锐二面角的平面角,进而可得结果.
所成锐二面角的平面角,进而可得结果.
试题解析:(1)证明:因为![]() 分别是Δ
分别是Δ![]() 的边
的边![]() 的中点,所以
的中点,所以![]() 经过
经过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,
, ![]()
![]()
又![]()
![]() ,
,![]()
![]() .
.
(2)证明:记![]()
![]()
![]() 且
且![]()
![]()
![]() ,
,![]() 四边形
四边形![]()
又![]()
![]() ,
,![]()
![]() .
.
![]()
![]() ,
,![]()
![]() 则得
则得![]() .
.
又![]() ,
,![]()
![]() .
.
(3) 过![]() ,易知
,易知![]() 是
是![]() 的中点,
的中点,
易知折叠后角![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]()
![]() ,
,
则可知![]() .
.
![]()
![]() .易知
.易知![]()
![]() 等腰
等腰![]() 的底角角
的底角角![]() 是
是![]() 所成锐二面角的平面角,
所成锐二面角的平面角,
易知角![]()
![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、面面垂直的判定定理、二面角的求法,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆E:
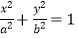 (a>b>0)的左右焦点分别为F1、F2 , D为椭圆短轴上的一个顶点,DF1的延长线与椭圆相交于G.△DGF2的周长为8,|DF1|=3|GF1|.
(a>b>0)的左右焦点分别为F1、F2 , D为椭圆短轴上的一个顶点,DF1的延长线与椭圆相交于G.△DGF2的周长为8,|DF1|=3|GF1|.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过椭圆E的左顶点A作椭圆E的两条互相垂直的弦AB、AC,试问直线BC是否恒过定点?若是,求出此定点的坐标;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面 为梯形,
为梯形,  底面
底面 ,
,  .过
.过 作一个平面
作一个平面 使得
使得 平面
平面 .
.(1)求平面
 将四棱锥
将四棱锥 分成两部分几何体的体积之比;
分成两部分几何体的体积之比;(2)若平面
 与平面
与平面 之间的距离为
之间的距离为 ,求直线
,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
:  (其中
(其中 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线 .
.(1)求曲线
 的方程;
的方程;(2)若点
 为曲线
为曲线 上一点,过点
上一点,过点 作曲线
作曲线 的切线交圆
的切线交圆 于不同的两点
于不同的两点 (其中
(其中 在
在 的右侧),已知点
的右侧),已知点 .求四边形
.求四边形 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的正半轴重合,两坐标系单位长度相同.已知曲线的极坐标方程为ρ=2cosθ+2sinθ,直线l的参数方程为
 (t为参数).
(t为参数).
(Ⅰ)将直线l的参数方程化为普通方程,将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设曲线C上到直线l的距离为d的点的个数为f(d),求f(d)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共
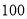 个,生产一个卫兵需
个,生产一个卫兵需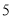 分钟,生产一个骑兵需
分钟,生产一个骑兵需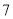 分钟,生产一个伞兵需
分钟,生产一个伞兵需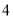 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过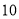 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润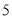 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润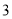 元.
元.(1)用每天生产的卫兵个数
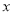 与骑兵个数
与骑兵个数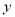 表示每天的利润
表示每天的利润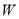 (元);
(元);(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
相关试题

