【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共![]() 个,生产一个卫兵需
个,生产一个卫兵需![]() 分钟,生产一个骑兵需
分钟,生产一个骑兵需![]() 分钟,生产一个伞兵需
分钟,生产一个伞兵需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润![]() 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润![]() 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润![]() 元.
元.
(1)用每天生产的卫兵个数![]() 与骑兵个数
与骑兵个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
参考答案:
【答案】(1)![]() ;(2)每天生产的卫兵个数为
;(2)每天生产的卫兵个数为![]() ,骑兵个数为
,骑兵个数为![]() ,伞兵个数为
,伞兵个数为![]() 时利润最大,最大利润为
时利润最大,最大利润为![]() 元..
元..
【解析】试题分析:(1)先写出每天生产的伞兵个数,列出利润w关于x的函数;
(2)由约束条件整理后画出可行域,写出目标函数,通过直线平移令w=0的直线,可经过点A时,w有最大值.求出点A的坐标,从而求得获得最大为利润.
试题解析:(1)依题意每天生产的伞兵个数为100-x-y,
所以利润w=5x+6y+3(100-x-y)=2x+3y+300.
(2)约束条件为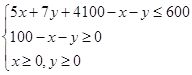
整理得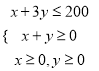
目标函数为w=2x+3y+300.
作出可行域.如图所示:
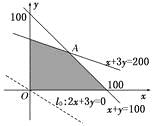
初始直线l0:2x+3y=0,平移初始直线经过点A时,w有最大值.
由![]() 得
得![]()
最优解为A(50,50),所以wmax=550元.
所以每天生产卫兵50个,骑兵50个,伞兵0个时利润最,最大为利润550元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下图中,四边形 ABCD是等腰梯形,
 ,
,  ,
, 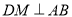 于M、交EF于点N,
于M、交EF于点N,  ,
,  ,现将梯形ABCD沿EF折起,记折起后C、D为
,现将梯形ABCD沿EF折起,记折起后C、D为 、
、 且使
且使 ,如图示.
,如图示.


(Ⅰ)证明:

 平面ABFE;,
平面ABFE;,(Ⅱ)若图6中,
 ,求点M到平面
,求点M到平面 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 (
( ),
), ,
,(Ⅰ) 试求曲线
 在点
在点 处的切线l与曲线
处的切线l与曲线 的公共点个数;(Ⅱ) 若函数
的公共点个数;(Ⅱ) 若函数 有两个极值点,求实数a的取值范围.
有两个极值点,求实数a的取值范围.(附:当
 ,x趋近于0时,
,x趋近于0时,  趋向于
趋向于 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程 .
.(1)若
 从
从 ,
,  ,
,  ,
,  四个数中任取的一个数,
四个数中任取的一个数, 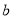 是从
是从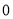 ,
,  ,
,  三个数中任取的一个数,求上述方程有实根的概率;
三个数中任取的一个数,求上述方程有实根的概率;(2)若
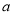 是从区间
是从区间 上任取的一个数,
上任取的一个数, 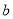 是从区间
是从区间 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某举重运动队为了解队员的体重分布情况,从50名队员中抽取10名作调查.抽取时现将全体队员随机按1~50编号,并按编号顺序平均分成10组,每组抽一名,且各组内抽取的编号依次增加5进行系统抽样.
(1)若第5组抽出的号码为22,写出所有被抽取出来的编号;
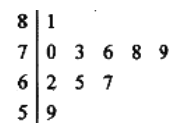
(2)分别统计被抽取的10名队员的体重(单位:公斤),获得如图所示的体重数据的茎叶图,根据茎叶图求该样本的平均数和中位数;
(3)在题(2)的茎叶图中,从题中不轻于73公斤的队员中随机抽取2名队员的体重数据,求体重为81公斤的队员被抽到的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4
 4:坐标系与参数方程
4:坐标系与参数方程在直角坐标系
 中,已知直线l1:
中,已知直线l1:  (
( ,
,  ),抛物线C:
),抛物线C:  (t为参数).以原点
(t为参数).以原点 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
相关试题

