【题目】极坐标系的极点在平面直角坐标系的原点O处,极轴与x轴的正半轴重合,两坐标系单位长度相同.已知曲线的极坐标方程为ρ=2cosθ+2sinθ,直线l的参数方程为 ![]() (t为参数).
(t为参数).
(Ⅰ)将直线l的参数方程化为普通方程,将曲线C的极坐标方程化为直角坐标方程;
(Ⅱ)设曲线C上到直线l的距离为d的点的个数为f(d),求f(d)的解析式.
参考答案:
【答案】解:(Ⅰ)直线l的参数方程为 ![]() (t为参数),消去参数,可得普通方程x+y﹣1=0;
(t为参数),消去参数,可得普通方程x+y﹣1=0;
曲线的极坐标方程为ρ=2cosθ+2sinθ,即ρ2=2ρcosθ+2ρsinθ,∴x2+y2﹣2x﹣2y=0;
(Ⅱ)x2+y2﹣2x﹣2y=0,可化为(x﹣1)2+(y﹣1)2=2,
圆心C(1,1)到直线l的距离为 ![]() =
= ![]() ,圆的半径为
,圆的半径为 ![]() ,
,
圆上的点到直线l距离d的取值范围是0≤d≤ ![]()
∴f(d)= 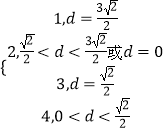
【解析】(Ⅰ)将直线l的参数方程消去参数,可得普通方程,将曲线C的极坐标方程,即ρ2=2ρcosθ+2ρsinθ,即可化为直角坐标方程;(Ⅱ)圆心C(1,1)到直线l的距离为 ![]() =
= ![]() ,圆的半径为
,圆的半径为 ![]() ,圆上的点到直线l距离d的取值范围是0≤d≤
,圆上的点到直线l距离d的取值范围是0≤d≤ ![]() ,即可求f(d)的解析式.
,即可求f(d)的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·江苏高考)如图,在三棱锥ABCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.

求证:(1)EF∥平面ABC;
(2)AD⊥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点
 分别是Δ
分别是Δ 的边
的边 的中点,连接
的中点,连接 .现将
.现将 沿
沿 折叠至Δ
折叠至Δ 的位置,连接
的位置,连接 .记平面
.记平面  与平面
与平面  的交线为
的交线为 ,二面角
,二面角 大小为
大小为 .
. 

(1)证明:

(2)证明:

(3)求平面
 与平面
与平面  所成锐二面角大小.
所成锐二面角大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 :
:  (其中
(其中 为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线
为圆心)上的每一点横坐标不变,纵坐标变为原来的一半,得到曲线 .
.(1)求曲线
 的方程;
的方程;(2)若点
 为曲线
为曲线 上一点,过点
上一点,过点 作曲线
作曲线 的切线交圆
的切线交圆 于不同的两点
于不同的两点 (其中
(其中 在
在 的右侧),已知点
的右侧),已知点 .求四边形
.求四边形 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某玩具生产公司每天计划生产卫兵、骑兵、伞兵这三种玩具共
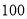 个,生产一个卫兵需
个,生产一个卫兵需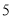 分钟,生产一个骑兵需
分钟,生产一个骑兵需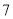 分钟,生产一个伞兵需
分钟,生产一个伞兵需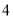 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过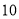 小时,若生产一个卫兵可获利润
小时,若生产一个卫兵可获利润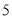 元,生产一个骑兵可获利润
元,生产一个骑兵可获利润 元,生产一个伞兵可获利润
元,生产一个伞兵可获利润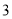 元.
元.(1)用每天生产的卫兵个数
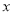 与骑兵个数
与骑兵个数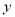 表示每天的利润
表示每天的利润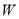 (元);
(元);(2)怎么分配生产任务才能使每天的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的几何体中,四边形
 是等腰梯形,
是等腰梯形,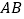 ∥
∥ ,
, 平面
平面 .
.(Ⅰ)求证:
 平面
平面 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|x+
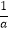 |+|x﹣a+1|(a>0是常数).
|+|x﹣a+1|(a>0是常数).
(Ⅰ)证明:f(x)≥1;
(Ⅱ)若f(3)<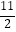 ,求a的取值范围.
,求a的取值范围.
相关试题

