Question

【题目】四棱柱的底面ABCD为矩形，AB＝1，AD＝2，，，则的长为( )

A． B． 　C． 　 　D．

Answer 1

【答案】C

【解析】分析：记A1在面ABCD内的射影为O，O在∠BAD的平分线上，说明∠BAD的平分线即菱形ABCD的对角线AC，求AC1的长．

解答：解：记A1在面ABCD内的射影为O，

∵∠A1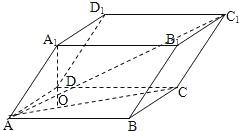AB=∠A1AD，
∴O在∠BAD的平分线上，
由O向AB，AD两边作垂线，垂足分别为E，F，连接A1E，A1F，A1E，A1F分别垂直AB，AD于E，F
∵AA1=3，∠A1AB=∠A1AD=60°，
∴AE=AF=
又四棱柱ABCD-A1B1C1D1的底面ABCD为矩形
∴∠OAF=∠OAE=45°，且OE=OF=，可得OA=
在直角三角形A1OA中，由勾股定理得A1O=
过C1作C1M垂直底面于M，则有△C1MC≌△A1OA，由此可得M到直线AD的距离是，M到直线AB的距离是，C1M=A1O=
所以AC1 ==
故选C．