【题目】如图,在多面体![]() 中,△
中,△![]() 是等边三角形,△
是等边三角形,△![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
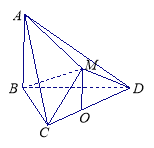
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
参考答案:
【答案】(1)证明略;(2)![]()
【解析】
试题分析:(1)因为△![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 为
为![]() 的中点,所以
的中点,所以![]() ,因为平面
,因为平面![]()
![]() 平面
平面![]() ,由面面垂直的性质定理得
,由面面垂直的性质定理得![]() 平面
平面![]() ,故得
,故得![]() ∥
∥![]() ,由线面平行的判定定理即得
,由线面平行的判定定理即得![]() ∥平面
∥平面![]() ;
;
(2)由(1)知![]() ∥平面
∥平面![]() ,所以
,所以![]() .
.
试题解析: (1)证明:
∵ △![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴ ![]() .
.
![]() ∵ 平面
∵ 平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
![]() ,
,
∴ ![]() 平面
平面![]()
∵ ![]()
![]() 平面
平面![]() ,
,
∴ ![]() ∥
∥![]()
∵ ![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]() ,
,
∴ ![]() ∥平面
∥平面![]()
(2):由(Ⅰ)知![]() ∥平面
∥平面![]() ,
,
∴ 点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
∵ ![]() ,△
,△![]() 是等边三角形,
是等边三角形,
∴ ![]() ,.
,.
连接![]() , 则
, 则![]() ,
, ![]() .
.
![]() =
=![]()
∴ 三棱锥![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次国际学术会议上,来自四个国家的五位代表被安排坐在一张圆桌,为了使他们能够自由交谈,事先了解到的情况如下:
甲是中国人,还会说英语.
乙是法国人,还会说日语.
丙是英国人,还会说法语.
丁是日本人,还会说汉语.
戊是法国人,还会说德语.
则这五位代表的座位顺序应为( )
A. 甲丙丁戊乙 B. 甲丁丙乙戊
C. 甲乙丙丁戊 D. 甲丙戊乙丁
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程.
已知曲线
 的参数方程为
的参数方程为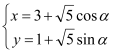 (
(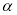 为参数),以直角坐标系原点为极点,
为参数),以直角坐标系原点为极点,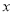 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.(1)求曲线
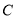 的极坐标方程;
的极坐标方程;(2)若直线的极坐标方程为
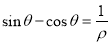 ,求直线被曲线
,求直线被曲线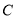 截得的弦长.
截得的弦长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)当
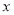 为常数,且
为常数,且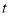 在区间
在区间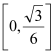 变化时,求
变化时,求 的最小值
的最小值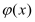 ;
;(2)证明:对任意的
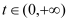 ,总存在
,总存在 ,使得
,使得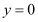 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
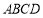 中,点
中,点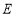 ,
,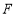 分别是
分别是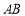 ,
,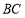 的中点,将
的中点,将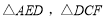 分别沿
分别沿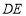 ,
,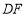 折起,使
折起,使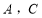 两点重合于
两点重合于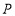 .
.
(Ⅰ)求证:平面
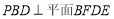 ;
;(Ⅱ)求二面角
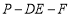 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 的方程为
的方程为 ,其中
,其中 .
. (1)求证:直线
 恒过定点;
恒过定点;(2)当
 变化时,求点
变化时,求点 到直线
到直线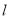 的距离的最大值;
的距离的最大值;(3)若直线
 分别与
分别与 轴、
轴、 轴的负半轴交于
轴的负半轴交于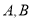 两点,求
两点,求 面积的最小值及此时直线
面积的最小值及此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2
 ,求圆的方程.
,求圆的方程.
相关试题

