【题目】已知直线![]() 的方程为
的方程为![]() ,其中
,其中![]() .
.
(1)求证:直线![]() 恒过定点;
恒过定点;
(2)当![]() 变化时,求点
变化时,求点![]() 到直线
到直线![]() 的距离的最大值;
的距离的最大值;
(3)若直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,求
两点,求![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
参考答案:
【答案】(1)见解析;(2)5;(3)见解析
【解析】试题分析:
(1)分离系数m,求解方程组可得直线恒过定点![]() ;
;
(2)结合(1)的结论可得点![]() 到直线
到直线![]() 的距离的最大值是5;
的距离的最大值是5;
(3)由题意得到面积函数: ![]()
![]() ,注意等号成立的条件.
,注意等号成立的条件.
试题解析:
(1)证明:直线![]() 方程
方程![]()
可化为![]()
该方程对任意实数![]() 恒成立,所以
恒成立,所以![]()
解得![]() ,所以直线恒过定点
,所以直线恒过定点![]()
(2)点![]() 与定点
与定点![]() 间的距离,就是所求点
间的距离,就是所求点![]() 到直线
到直线![]() 的距离的最大值,即
的距离的最大值,即![]()
(3)由于直线![]() 过定点
过定点![]() ,分别与
,分别与![]() 轴,
轴, ![]() 轴的负半轴交于
轴的负半轴交于![]() 两点,
两点,
设其方程为![]() ,则
,则![]()
所以![]()
![]()
当且仅当![]() 时取等号,面积的最小值为4
时取等号,面积的最小值为4
此时直线![]() 的方程为
的方程为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(1)当
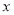 为常数,且
为常数,且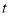 在区间
在区间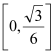 变化时,求
变化时,求 的最小值
的最小值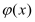 ;
;(2)证明:对任意的
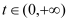 ,总存在
,总存在 ,使得
,使得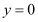 .
. -
科目: 来源: 题型:
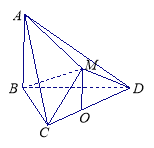
查看答案和解析>>【题目】如图,在多面体
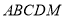 中,△
中,△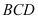 是等边三角形,△
是等边三角形,△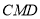 是等腰直角三角形,
是等腰直角三角形, ,平面
,平面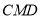
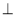 平面
平面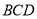 ,
,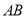
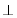 平面
平面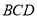 ,点
,点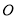 为
为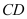 的中点,连接
的中点,连接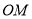 .
.
(1)求证:
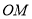 ∥平面
∥平面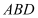 ;
;(2)若
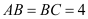 ,求三棱锥
,求三棱锥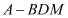 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
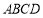 中,点
中,点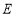 ,
,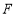 分别是
分别是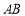 ,
,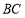 的中点,将
的中点,将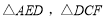 分别沿
分别沿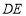 ,
,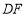 折起,使
折起,使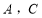 两点重合于
两点重合于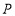 .
.
(Ⅰ)求证:平面
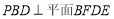 ;
;(Ⅱ)求二面角
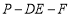 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设圆上的点A(2,3)关于直线x+2y=0的对称点仍在圆上,且直线x-y+1=0被圆截得的弦长为2
 ,求圆的方程.
,求圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
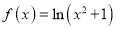 ,
, 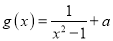
(1)若
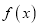 的一个极值点到直线
的一个极值点到直线 的距离为1,求
的距离为1,求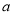 的值;
的值;(2)求方程
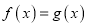 的根的个数
的根的个数 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
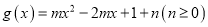 在
在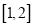 上有最大值1和最小值0,设
上有最大值1和最小值0,设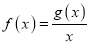 .
.(1)求
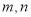 的值;
的值;(2)若不等式
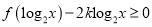 在
在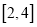 上有解,求实数
上有解,求实数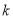 的取值范围;
的取值范围;(3)若方程
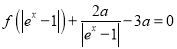 (
(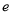 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数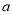 的取值范围.
的取值范围.
相关试题

