【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() .
.
(Ⅰ)若数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若![]() ,
, ![]() ,且
,且![]() .
.
(i)求![]() 的值;
的值;
(ii)对于数列![]() 和
和![]() ,满足关系式
,满足关系式![]() ,
, ![]() 为常数,且
为常数,且![]() ,求
,求![]() 的最大值.
的最大值.
参考答案:
【答案】(Ⅰ)a=2,b=-2;(Ⅱ)(i)a=2, (ii)![]()
【解析】试题分析:(Ⅰ)令![]() 代入
代入![]() 求出
求出![]() ,
, ![]() ,由
,由![]() 求出
求出![]() ;
;
(Ⅱ)(i)证明:因为![]() ,
, ![]() ,
,
又![]() ,因为
,因为![]() ,
, ![]() 均为正整数,可得
均为正整数,可得![]() ,
, ![]()
当![]() ,
, ![]() 时,推出矛盾. 所以
时,推出矛盾. 所以![]()
(ii)由题![]() 可得
可得![]() 因为
因为![]() ,
, ![]() 均为正整数,
均为正整数, ![]() 为常数,
为常数,
所以当且仅当![]() 时,
时, ![]() 有最大值是
有最大值是![]()
试题解析:(Ⅰ)因为![]() ,
,
所以![]()
因为![]()
所以公差![]()
(Ⅱ)(i)证明:因为![]() ,
, ![]() ,
,
又![]() ,
,
所以![]()
因为![]() ,
, ![]() 均为正整数,且
均为正整数,且![]() ,
, ![]() ,
,
所以![]()
所以![]() ,
, ![]()
又![]() ,所以
,所以![]()
当![]() ,
, ![]() 时,有
时,有![]() ,产生矛盾.
,产生矛盾.
所以![]()
(ii)因为![]() ,所以
,所以![]()
所以![]()
因为![]() ,
, ![]() 均为正整数,
均为正整数, ![]() 为常数,
为常数,
所以当且仅当![]() 时,
时, ![]() 有最大值是
有最大值是![]()
所以![]() 的最大值是
的最大值是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某次有600人参加的数学测试,其成绩的频数分布表如图所示,规定85分及其以上为优秀.
区间
[75,80)
[80,85)
[85,90)
[90,95)
[95,100]
人数
36
114
244
156
50
(Ⅰ)现用分层抽样的方法从这600人中抽取20人进行成绩分析,求其中成绩为优秀的学生人数;
(Ⅱ)在(Ⅰ)中抽取的20名学生中,要随机选取2名学生参加活动,记“其中成绩为优秀的人数”为
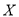 ,求
,求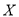 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱柱
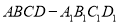 中,
中, 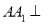 平面
平面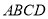 ,底面
,底面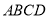 为梯形,
为梯形, 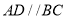 ,
, 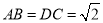 ,
, 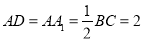 ,点
,点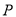 ,
, 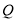 分别为
分别为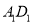 ,
, 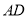 的中点.
的中点. 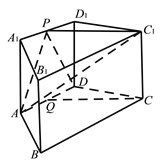
(Ⅰ)求证:
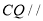 平面
平面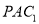 ;
; (Ⅱ)求二面角
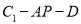 的余弦值;
的余弦值; (Ⅲ)在线段
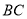 上是否存在点
上是否存在点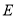 ,使
,使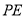 与平面
与平面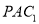 所成角的正弦值是
所成角的正弦值是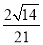 ,若存在,求
,若存在,求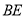 的长;若不存在,请说明理由.
的长;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)当
 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)对任意的
 ,
,  恒成立,求
恒成立,求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量
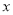 分布在
分布在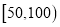 内,且销售量
内,且销售量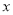 的分布频率
的分布频率 .
.(Ⅰ)求
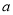 的值并估计销售量的平均数;
的值并估计销售量的平均数;(Ⅱ)若销售量大于等于70,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取8天,再从这8天中随机抽取3天进行统计,设这3天来自
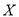 个组,求随机变量
个组,求随机变量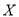 的分布列及数学期望(将频率视为概率).
的分布列及数学期望(将频率视为概率). -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,在空间直角坐标系
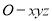 中,正四面体(各条棱均相等的三棱锥)
中,正四面体(各条棱均相等的三棱锥)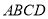 的顶点
的顶点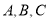 分别在
分别在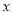 轴,
轴, 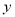 轴,
轴, 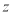 轴上.
轴上.
(Ⅰ)求证:
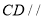 平面
平面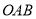 ;
;(Ⅱ)求二面角
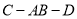 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系
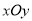 中,直线
中,直线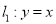 与直线
与直线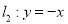 之间的阴影部分即为
之间的阴影部分即为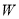 ,区域
,区域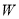 中动点
中动点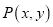 到
到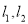 的距离之积为1.
的距离之积为1.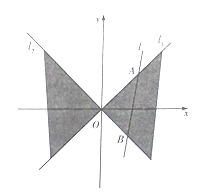
(Ⅰ)求点
 的轨迹
的轨迹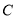 的方程;
的方程;(Ⅱ)动直线
 穿过区域
穿过区域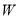 ,分别交直线
,分别交直线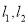 于
于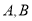 两点,若直线
两点,若直线 与轨迹
与轨迹 有且只有一个公共点,求证:
有且只有一个公共点,求证: 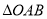 的面积恒为定值.
的面积恒为定值.
相关试题

